题目内容
19. 已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=$\frac{1}{2}$BE.
已知,Rt△ABC中,∠ACB=90°,AC=BC,∠ABC的角平分线交AC于E,AD⊥BE于D,求证:AD=$\frac{1}{2}$BE.
分析 延长AD和BC交于F,求出∠CBE=∠CAF,AC=BC,证△EBC≌△FAC,△ABD≌△FBD,推出BE=AF,AD=DF,即可得出答案.
解答 解:如图延长AD和BC交于F,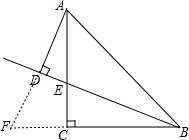
∵Rt△ABC中,∠ACB=90°,∠BAC=45°,
∴∠ABC=45°=∠BAC,
∴AC=BC,
∵∠ACB=90°,
∴∠BCE=∠ACF=90°,
∵BE平分∠ABC,
∴∠ABD=∠EBC,
∵BD⊥AD,
∴∠BCE=∠ADE=90°,
∵∠BEC=∠AED,
∴根据三角形内角和定理得:∠DAE=∠CBE,
在△BCE和△ACF中,
$\left\{\begin{array}{l}{∠FAC=∠CBE}\\{AC=BC}\\{∠ACF=∠BCE}\end{array}\right.$,
∴△BCE≌△ACF(SAS),
∴BE=AF,
在△ABD和△FBD中,
$\left\{\begin{array}{l}{∠ABD=∠FBD}\\{BD=BD}\\{∠ADB=∠FDB}\end{array}\right.$,
∴△ABD≌△FBD(ASA),
∴AD=DF,
即AF=2AD,
∴AD=$\frac{1}{2}$AF,
∴AD=$\frac{1}{2}$BE.
点评 本题考查了全等三角形的性质和判定的应用,解此题的关键是求出BE=AF和AD=DF,题目比较好,难度适中.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14. 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )| A. | 2.2 | B. | 2.5 | C. | 2 | D. | 1.8 |
4.某食品加工厂生产标准质量为每袋80g(±5g)的袋装方便而,其中“(±5g)”的含义是:如果每袋方便面的质量比标准质量多(或者差)5g以上即视为不合格产品,如:实际质量为85g的方便面是合格产品.现从中抽出样品20袋,检测每袋的质量是否符合标准,检测记录如表:(用正数表示超出部分,用负数表示不足部分,单位:g)
(1)抽出的样品中质量不合格的有多少袋?
(2)抽出的样品一共有多少g?
| 与标准质量的差值 | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 袋数 | 1 | 0 | 2 | 2 | 2 | 3 | 3 | 2 | 2 | 0 | 1 | 1 | 1 |
(2)抽出的样品一共有多少g?
11.新华购物中心新购进篮球和排球共30个,进价和售价如表,全部销售完后共获利润510元.
(1)购进篮球和排球各多少个?
(2)销售8个排球的利润与销售几个篮球的利润相等?
| 篮球 | 排球 | |
| 进价(元/个) | 95 | 80 |
| 售价(元/个) | 110 | 100 |
(2)销售8个排球的利润与销售几个篮球的利润相等?
9.已知x=3是一元二次方程2x2+mx+15=0的一个解,则方程的另一个解是( )
| A. | $\frac{5}{2}$ | B. | -$\frac{5}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
 如图,已知△ABC是等边三角形,且CE=AD.求证:DF=EF.
如图,已知△ABC是等边三角形,且CE=AD.求证:DF=EF. 已知,如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{2}{5}$∠AOE,求∠EOG和∠DOF的度数.
已知,如图,直线AB、CD、EF都经过点O,且AB⊥CD,OG平分∠BOE,如果∠EOG=$\frac{2}{5}$∠AOE,求∠EOG和∠DOF的度数.