题目内容
2. 已知平行四边形ABCD,AC与BD交于O点,EF过点O且EF⊥AB,AC=$\sqrt{5}$EF,∠ACB=45°.
已知平行四边形ABCD,AC与BD交于O点,EF过点O且EF⊥AB,AC=$\sqrt{5}$EF,∠ACB=45°.(1)图中有6对全等三角形;
(2)求证:OA平分∠DOE;
(3)求S四边形ADOE:S四边形ABCD.
分析 (1)根据平行四边形的性质可得出OA=OC,OB=OD,根据全等三角形的判定方法可得出6对全等三角形;
(2)根据EF⊥AB,可得出OA=$\sqrt{5}$OE,根据勾股定理即可得出AE=2OE=EF,作AH⊥CD,交CD的延长线于H,得四边形AEFH为正方形,求得AE=AH,△ADH顺时针旋转90°,使H与E重合,得到△AGE,从而得到∠HAD=∠EAG,AG=AD,进一步求得∠GAO=∠DAO=45°,然后根据SAS证得△AOD≌△AOG,即可证得结论;
(3)由(2)可知OD=OE+DH,设OE=OF=a,DH=a,则OD=a+x,DF=2a-x,在RT△ODF中利用勾股定理求出a与x的关系可以解决问题.
解答 解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AD=BC,AB=CD,AB∥CD,
∴∠OAE=∠OCF,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS),
同理可得:△BOE≌△DOF,
在△AOD和△COB中,
$\left\{\begin{array}{l}{OA=OC}\\{AD=CB}\\{OD=OB}\end{array}\right.$,
∴△AOD≌△COB(SSS),
同理可得:△AOB≌△COD,△ACD≌△CAB,△ABD≌△CDB.
故答案为:6;
(2)如图1,∵AC=$\sqrt{5}$EF,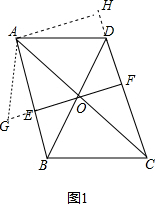 ∴OA=$\sqrt{5}$OE,
∴OA=$\sqrt{5}$OE,
∵AE2=OA2-OE2,
∴AE2=4OE2,
∴AE=2OE,
∴AE=EF,
作AH⊥CD,交CD的延长线于H,得四边形AEFH为正方形,
∴AE=AH,
延长FE到G,使EG=DH,连接AG,
∴△ADH≌△AGE(SAS),
∴∠HAD=∠EAG,AG=AD,
∵∠ACB=∠DAC=45°,
∵AH⊥AE,
∴∠HAD+∠EAO=45°,
∴∠GAO=∠DAO=45°,
在△AOD和△AOG中
$\left\{\begin{array}{l}{AG=AD}\\{∠GAO=∠DAO}\\{OA=OA}\end{array}\right.$
∴△AOD≌△AOG(SAS),
∴∠AOD=∠AOE,
∴OA平分∠DOE;
(3)设OE=OF=a,DH=x,由(2)可知DO=OG=OE+EG=OE+DH=a+x,AE=HF=2a,DF=2a-x,
在RT△DOF中,∵DO2=OF2+DF2,
∴(a+x)2=a2+(2a-x)2,
∴X=$\frac{2}{3}a$,易知:DF=EB=2a-$\frac{2}{3}$a=$\frac{4}{3}$a,
∴AE:EB=3:2,
∵ABCD是平行四边形,
∴可以设S△AOD=S△AOB=5K,则易知:S平行四边形ABCD=20K,S△AOE=3K,
∴S四边形ADOE=8K,
∴S四边形ADOE:S平行四边形ABCD=8K:20K=2:5.
点评 此题考查了平行四边形,正方形的性质以及利用勾股定理解决边之间的关系.注意45°角在本题目中的作用.

 阅读快车系列答案
阅读快车系列答案 为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
为估计池塘两岸A,B间的距离,杨阳在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )| A. | 15m | B. | 17m | C. | 20m | D. | 28m |
| A. | -|-5|=5 | B. | -2(a+3b)=-2a+6b | C. | 3m+2n=5mn | D. | x2y-2x2y=-x2y |
 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则DE的长为( )| A. | 2.2 | B. | 2.5 | C. | 2 | D. | 1.8 |
| 篮球 | 排球 | |
| 进价(元/个) | 95 | 80 |
| 售价(元/个) | 110 | 100 |
(2)销售8个排球的利润与销售几个篮球的利润相等?
 如图,已知△ABC是等边三角形,且CE=AD.求证:DF=EF.
如图,已知△ABC是等边三角形,且CE=AD.求证:DF=EF.