Question

11．如图，抛物线y=$\frac{1}{2}$x²+bx-2与x轴交于A、B两点，与y轴交于C点，且A（-1，0），点M（m，0）是x轴上的一个动点，
（1）判断△ABC的形状，证明你的结论；
（2）当CM+DM的值最小时，求m的值．

Answer 1

分析 （1）由点A（-1，0）在抛物线$y=\frac{1}{2}{x^2}+bx-2$上，求得b=-$\frac{3}{2}$，得出抛物线的解析式为y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2，求出C（0，-2），A（-1，0），B（4，0），由AC²+BC²=AB²，得出△ABC是直角三角形；
（2）作点C关于x轴的对称点C′，连接C′D交x轴于点M，求出二次函数的顶点坐标与C关于x轴的对称点C′，根据轴对称性及两点之间线段最短，求得直线C′D的解析式，与x轴的交点的横坐标即是m的值．

解答 解：（1）△ABC是直角三角形，理由如下：
∵点A（-1，0）在抛物线$y=\frac{1}{2}{x^2}+bx-2$上，
∴$\frac{1}{2}{（-1）^2}+b（-1）-2=0$，
解得：b=-$\frac{3}{2}$，
∴抛物线的解析式为：y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2，
∴当x=0时，y=-2，
∴C（0，-2），即OC=2，
当y=0时，$\frac{1}{2}{x^2}-\frac{3}{2}x-2=0$，
解得：x₁=-1，x₂=4，
∴A（-1，0），B（4，0），
即：OA=1，OB=4，AB=5．
∴AB²=25，AC²=OA²+OC²=1²+2²=5，BC²=OC²+OB²=2²+4²=20，
∴AC²+BC²=AB²，
∴△ABC是直角三角形；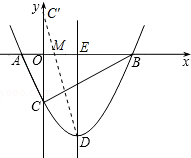
（2）作点C关于x轴的对称点C′，
则C′（0，2），OC′=2，连接C′D交x轴于点M，如图所示：
根据轴对称性及两点之间线段最短可知，MC+MD的最小值为线段C'D，
∵抛物线y=$\frac{1}{2}$x²-$\frac{3}{2}$x-2=$\frac{1}{2}$（x-$\frac{3}{2}$）²-$\frac{25}{8}$，
∴抛物线的顶点$D（\frac{3}{2}，-\frac{25}{8}）$
设直线C'D解析式：y=kx+b（k≠0），则$\left\{\begin{array}{l}b=2\\ \frac{3}{2}k+b=-\frac{25}{8}\end{array}\right.$，
解得：k=-$\frac{41}{12}$，b=2，
∴直线C'D解析式：y=-$\frac{41}{12}$x+2，
当y=0时，得x=$\frac{24}{41}$，
∴m=$\frac{24}{41}$．

点评 本题考查了抛物线与x轴的交点、抛物线解析式的求法、抛物线的顶点坐标、轴对称的性质、待定系数法求直线的解析式、勾股定理的逆定理、最小值问题等知识；本题综合性强，有一定难度．