题目内容
12.已知x1、x2是关于x的方程x2+m2x+n=0(n<0)的两个实数根,y1、y2是关于y的方程y2+5my+7=0的两个实数根,且x1-y1=2,x2-y2=2,求m的值.分析 根据根与系数的关系得到x1+x2=-m2y1+y2=-5m,再把x1-y1=2和x2-y2=2相加得到x1+x2-(y1+y2)=4,所以-m2+5m=4,解方程得到m=4或m=1,然后根据判别式的意义判断满足条件的m的值.
解答 解:根据题意得x1+x2=-m2y1+y2=-5m,
∵x1-y1=2,x2-y2=2,
∴x1+x2-(y1+y2)=4,
∴-m2+5m=4,
整理得m2-5m+4=0,解得m=4或m=1,
而m=1时,方程y2+5y+7=0没有实数根,故m=1舍去.
∴m的值为4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
相关题目
7. 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=CD,AC=BD | B. | AB=CD,∠ABC=∠BCD | C. | ∠ABC=∠DCB,∠A=∠D | D. | AB=CD,∠A=∠D |
17.二次函数y=-2(x+2)2-3的图象的顶点坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
1.下列函数中,能表示y是x的反比例函数的是( )
| A. | y=$\frac{1}{2x}$ | B. | y=$\frac{1}{x-1}$ | C. | y=2x | D. | y=$\frac{2}{\sqrt{x}}$ |
 已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.
已知两条直线l1、l2分别经过点A(-1,0)、点B(3,0)并且当两条直线同时相交于y轴的负半轴上的点C时,恰好有l1⊥l2,经过点A、B、C的抛物线的对称轴与直线l1交于点K,与直线l2交于点E,在x轴交于点F,D是抛物线的顶点,如图所示.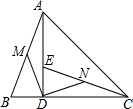 如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点. 如图,△ABC,AB=AC,点D在AC上,DA=DB=BC,则∠BDA=108度.
如图,△ABC,AB=AC,点D在AC上,DA=DB=BC,则∠BDA=108度.