题目内容
8. 已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
分析 先判断出,∠2=∠A,∠3=∠1,进而判断出∠1=∠2,即可判断出△OED≌△OBD即可得出DE⊥OE,即可得出结论.
解答  解:连接OD,OE,
解:连接OD,OE,
∵O,D分别是AB,BC中点,
∴OD∥AC,
∴∠2=∠A,∠3=∠1,
∵OA=OE,
∴∠A=∠3,
∴∠1=∠2,
在△OED和△OBD中,$\left\{\begin{array}{l}{OE=OB}\\{∠1=∠2}\\{OD=OD}\end{array}\right.$,
∴△OED≌△OBD,
∴∠OED=∠ABC=90°,
∴DE⊥OE,
∵点D在⊙O上,
∴DE与⊙O相切.
点评 此题是切线的判定,主要考查了平行线的性质和判定,全等三角形的判定和性质,解本题的关键是判断出,△OED≌△OBD.

练习册系列答案
相关题目
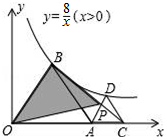 如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
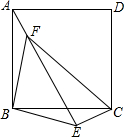 点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE、FC的长.
点E在正方形ABCD外,BE=4,CE=2,∠BEC=135°,将△BEC绕点B逆时针旋转得到△BFA,求FE、FC的长. 如图所示,用代数式表示图中阴影部分的面积,并计算x=6时,阴影部分的面积.(π取3.14)
如图所示,用代数式表示图中阴影部分的面积,并计算x=6时,阴影部分的面积.(π取3.14)