题目内容
16.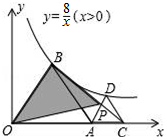 如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
如图,△AOB和△ACD均为正三角形,顶点B、D在双曲线y=$\frac{8}{x}$(x>0)上,线段BC、AD交于点P,则S△OBP=8.
分析 先根据△AOB和△ACD均为正三角形可知∠AOB=∠CAD=60°,故可得出AD∥OB,所以S△ABP=S△AOP,故S△OBP=S△AOB,过点B作BE⊥OA于点E,由反比例函数系数k的几何意义即可得出结论.
解答 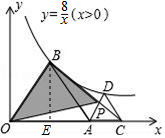 解:∵△AOB和△ACD均为正三角形,
解:∵△AOB和△ACD均为正三角形,
∴∠AOB=∠CAD=60°,
∴AD∥OB,
∴S△ABP=S△AOP,
∴S△OBP=S△AOB,
过点B作BE⊥OA于点E,则S△OBE=S△ABE=$\frac{1}{2}$S△AOB,
∵点B在反比例函数y=$\frac{8}{x}$的图象上,
∴S△OBE=$\frac{1}{2}$×8=4,
∴S△OBP=S△AOB=2S△OBE=8.
故答案为:8.
点评 本题考查的是反比例函数系数k的几何意义,涉及到等边三角形的性质、三角形的面积等知识,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.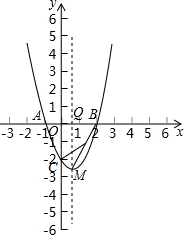 已知二次函数的图象如图所示,抛物线与x轴、y轴分别交于点A(-1,0)、B(2,0)、C(0,-2).
已知二次函数的图象如图所示,抛物线与x轴、y轴分别交于点A(-1,0)、B(2,0)、C(0,-2). 已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.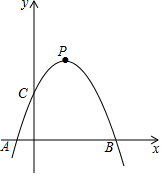 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,点A的横坐标为-1.与y轴交于点C,点C的纵坐标为2.顶点为P.过动点H (0,m)作平行于x轴的直线l,直线l与抛物线相交于点D、E.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,点A的横坐标为-1.与y轴交于点C,点C的纵坐标为2.顶点为P.过动点H (0,m)作平行于x轴的直线l,直线l与抛物线相交于点D、E.