题目内容
20.已知抛物线y=x2-2x-3.(1)直接写出抛物线的开口方向、对称轴和顶点坐标;
(2)若抛物线与x轴的两个交点为A、B,与y轴的一个交点为C,画草图,求△ABC的面积.
分析 (1)利用配方法将抛物线的标准式变形为顶点式,结合二次项系数为1即可得出结论;
(2)利用十字相乘法将抛物线的标准式变形为交点式,由此即可得出点A、B的坐标,将x=0代入抛物线解析式求出y值,进而得出点C的坐标,再根据三角形的面积公式求出△ABC的面积即可.
解答 解:(1)∵y=x2-2x-3=(x-1)2-4,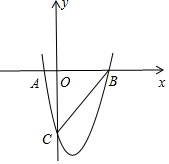
∴该抛物线开口向上,对称轴为x=1,顶点坐标为(1,-4).
(2)按点A在点B的左侧画出草图,如图所示.
∵y=x2-2x-3=(x+1)(x-3),
∴点A(-1,0),点B(3,0),
当x=0时,y=-3,
∴点C(0,-3),
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×[3-(-1)]×|-3|=6.
点评 本题考查了抛物线与x轴的交点、二次函数图象上点的坐标以及三角形的面积公式,根据二次函数图象上点的坐标特征求出点A、B、C的坐标是解题的关键.

练习册系列答案
相关题目
12.下列各组数中,相等的一组是( )
| A. | -(-2)3和-23 | B. | (-2)2和-22 | C. | -(-2)和-2 | D. | |-2|3和|2|3 |
 四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$.
四点A、C、B、D顺次在一直线上,设AB=a,AC=b,AD=c,并且$\frac{1}{b}$+$\frac{1}{c}$=$\frac{2}{a}$,求证:$\frac{AC}{BC}$=$\frac{AD}{BD}$. 已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
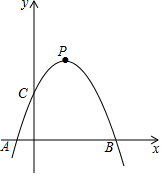 如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,点A的横坐标为-1.与y轴交于点C,点C的纵坐标为2.顶点为P.过动点H (0,m)作平行于x轴的直线l,直线l与抛物线相交于点D、E.
如图,在平面直角坐标系xOy中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于点A、B,点A的横坐标为-1.与y轴交于点C,点C的纵坐标为2.顶点为P.过动点H (0,m)作平行于x轴的直线l,直线l与抛物线相交于点D、E.