题目内容
17.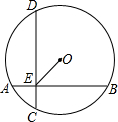 如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.
如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.
分析 连接OB,作ON⊥CD,OM⊥AB,转化到直角三角形中解答.
解答 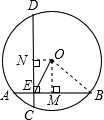 解:AB=AE+BE=5+13=18(cm),
解:AB=AE+BE=5+13=18(cm),
连接OB,过O作OM⊥AB,
∴AM=$\frac{1}{2}$AB=9(cm),
又∵OM=2$\sqrt{10}$(cm),
∴在Rt△OBM中,
BO=$\sqrt{O{M}^{2}+B{M}^{2}}$=$\sqrt{81+40}$=$\sqrt{121}$=11cm,
ON=EM=AM-AE=9-5=4(cm),
∴OE=$\sqrt{O{M}^{2}+E{M}^{2}}$=$\sqrt{(2\sqrt{10})^{2}+{4}^{2}}$=2$\sqrt{14}$.
点评 本题考查的是垂径定理,勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
12. 如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
 如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )
如图,∠A=∠DBC=90°,AD=3,AB=4,BC=12,则CD的长为( )| A. | 5 | B. | 13 | C. | 17 | D. | 19 |
7. 一次函数y=kx-b的图象如图所示,那么点(-2k,b)所在的象限是( )
一次函数y=kx-b的图象如图所示,那么点(-2k,b)所在的象限是( )
 一次函数y=kx-b的图象如图所示,那么点(-2k,b)所在的象限是( )
一次函数y=kx-b的图象如图所示,那么点(-2k,b)所在的象限是( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分:
如图,AB∥CD,∠B=26°,∠D=39°,求∠BED的度数.完成以下解答过程中的空缺部分: