题目内容
8.古运河是扬州的母亲河,为打造古运河风光带,现有一段河道整治任务由A、B两工程队完成.A工程队单独整治该河道要16天才能完成;B工程队单独整治该河道要24天才能完成.现在A工程队单独做6天后,B工程队加入合做完成剩下的工程,问A工程队一共做了多少天?分析 设A工程队一共做的天数为x天,根据工作总量为“1”列出方程并解答.
解答 解:设A工程队一共做的天数为x天,则
由题意得:$\frac{1}{16}$x+$\frac{1}{24}$(x-6)=1,
解得:x=12
答:A工程队一共做的天数为12天.
点评 本题考查了一元一次方程的应用,解答本题的关键是表示出两工程队的工作效率,根据工作总量为单位1,建立方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.图中阴影部分的面积相等的是( )


| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | 无法判断 |
18. 如图,数轴上点C表示实数是-2,O为原点,BC⊥OC,且BC=1,以点O为圆心,OB长为半径作弧,交数轴负半轴于点A,则点A表示的实数是( )
如图,数轴上点C表示实数是-2,O为原点,BC⊥OC,且BC=1,以点O为圆心,OB长为半径作弧,交数轴负半轴于点A,则点A表示的实数是( )
 如图,数轴上点C表示实数是-2,O为原点,BC⊥OC,且BC=1,以点O为圆心,OB长为半径作弧,交数轴负半轴于点A,则点A表示的实数是( )
如图,数轴上点C表示实数是-2,O为原点,BC⊥OC,且BC=1,以点O为圆心,OB长为半径作弧,交数轴负半轴于点A,则点A表示的实数是( )| A. | -2.2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | -2.5 |
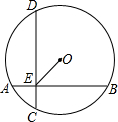 如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.
如图,⊙O的弦AB、CD互相垂直于E,AE=5cm,BE=13cm,O到AB的距离为2$\sqrt{10}$cm.求O到CD的距离,OE的长及⊙O的半径.