题目内容

13．已知在△ABC中，AB=AC=5，BC=6，AD是BC边上的中线，四边形ADBE是平行四边形．
求证：平行四边形ADBE是矩形．

分析 利用三线合一定理可以证得∠ADB=90°，再根据矩形的定义即可证得．

解答 证明：∵AB=AC，AD是BC的边上的中线，
∴AD⊥BC，
∴∠ADB=90°，
∵四边形ADBE是平行四边形，
∴平行四边形ADBE是矩形．

点评 本题考查了三线合一定理以及矩形的判定，理解三线合一定理是关键．

练习册系列答案
相关题目
3．已知x2=25，那么x=±5；如果（-a）2=（-6）2，那么a=±6．
4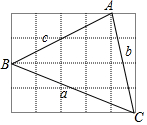．如图所示，在正方形网格中，每个小正方形的边长为1，则网格上的△ABC（△ABC的各项点均在格点上）的三边a、b、c之间的大小关系是（　　）
A．c＜a＜bB．b＜c＜aC．c＜b＜aD．a＜c＜b
1．有下列各数，0.01，10，-6.6.7，-$\frac{1}{3}$，0，-90，-（-3），-|-2|，|-4|，其中属于非负整数的共有（　　）
A．1个B．2个C．3个D．4个
8．如图，下列条件中，能判断AB∥CD的是（　　）
A．∠1=∠2B．∠3=∠4C．∠BAC=∠BCDD．∠ABC+∠BAD=180°
18．如果两条平行线被三条直线所截，那么一对内错角的角平分线一定（　　）
A．互相平行B．互相垂直C．相交成锐角D．相交成钝角
5．如图，在△ABC中，把△ABC沿直线AD翻折180°，使点C 落在点B的位置，则线段AD是（　　）
A．边BC上的中线B．边BC上的高C．∠BAC的平分线D．以上都是
2．如图，四边形ABCD是菱形，∠DAB=50°，对角线AC，BD相交于点O，DH⊥AB于H，连接OH，则∠DHO的度数是（　　）
A．20°B．25°C．30°D．35°
3．在二次根式$\sqrt{x-2}$中，字母x的取值范围是（　　）
A．x＞2B．x＜2C．x≥2D．x≤2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网