题目内容
2．将a=（-99）0，b=（-0.1）-1，$c={（{-\frac{5}{3}}）^{-2}}$，这三个数从小到大的顺序排为b＜c＜a．分析 首先分别求出这三个数的大小，然后根据实数比较大小的方法，把这三个数从小到大的顺序排列起来即可．
解答 解：∵a=（-99）0=1；b=（-0.1）-1=${（-\frac{1}{10}）}^{-1}$=-10；）-1，$c={（{-\frac{5}{3}}）^{-2}}$=${（-\frac{5}{3}）}^{-2}$=$\frac{1}{{（-\frac{5}{3}）}^{2}}$=$\frac{9}{25}$，
∴b＜c＜a，
故答案为：b＜c＜a．
点评 此题主要考查了实数比较大小的方法和负整数指数幂的运算，运用负整数指数幂的运算法则分别求出这三个数的大小是解答此题的关键．
练习册系列答案
相关题目
12．已知A、B两地相距630千米，在A、B之间有汽车站C站，如图1所示．客车由A地驶向C站、货车由B地驶向A地，两车同时出发，匀速行驶，货车的速度是客车速度的$\frac{3}{4}$．图2是客、货车离C站的路程y1、y2（千米）与行驶时间x（小时）之间的函数关系图象．则下列说法不正确的是（ ）
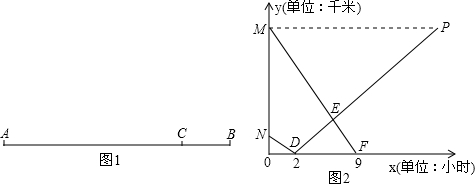
| A． | 货车行驶2小时到达C站 | B． | 货车行驶完全程用时14小时 | ||
| C． | 图2中的点E的坐标是（7，180） | D． | 客车的速度是60千米∕时 |
13．下列计算中，正确的是（ ）
| A． | $\sqrt{8}-\sqrt{2}=\sqrt{6}$ | B． | $\sqrt{8}+\sqrt{2}=\sqrt{10}$ | C． | $\sqrt{8}÷\sqrt{2}=4$ | D． | $\sqrt{8}×\sqrt{2}=4$ |
11．已知A，B，C三个数，其中A=-$\frac{\sqrt{2}}{2}$，B=0，C=-$\frac{1}{\sqrt{3}}$，则A，B，C的大小关系是（ ）
| A． | C＞A＞B | B． | B＞A＞C | C． | C＞B＞A | D． | B＞C＞A |