题目内容
10. 如图,在菱形ABCD中,对角线AC=6,BD=2,以D为圆心,DA为半径作圆,过点B作AC的平行线交⊙D于M,N,则MN的长是2$\sqrt{6}$.
如图,在菱形ABCD中,对角线AC=6,BD=2,以D为圆心,DA为半径作圆,过点B作AC的平行线交⊙D于M,N,则MN的长是2$\sqrt{6}$.
分析 先由菱形的性质得出直角,用勾股定理求出半径AD,再由平行线得出直角三角形,最后用勾股定理求出BM即可.
解答 解:如图,
连接DM,
在菱形ABCD中,对角线AC=6,BD=2,
∴AD=$\sqrt{10}$,
∵MN∥AC,
∴∠DBM=90°,
∴BM=$\sqrt{D{M}^{2}-B{D}^{2}}$=$\sqrt{6}$,
∴MN=2BM=2$\sqrt{6}$,
故答案为2$\sqrt{6}$.
点评 此题是菱形的性质,主要考查了菱形的性质,圆的性质,垂定定理,勾股定理,解本题关键是构造直角三角形.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.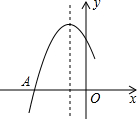 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,下列结论:①b2>4ac;
②2a+b=0;
③a+b+c>0;
④若B(-5,y1)、C(-1,y2 )为函数图象上的两点,则y1<y2.
其中正确结论是( )
| A. | ②④ | B. | ①③④ | C. | ①④ | D. | ②③ |
18.如果一个长方形的长减少4cm,宽增加2cm,所得的四边形是一个正方形,且该正方形的面积与原长方形的面积相等,则原长方形的面积为( )
| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
15.在△ABC中,AB=3,AC=2.当∠B最大时,BC的长是( )
| A. | 1 | B. | 5 | C. | $\sqrt{13}$ | D. | $\sqrt{5}$ |
2. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD,若∠ABC+∠ADC=120°,则∠A的度数是( )| A. | 100° | B. | 110° | C. | 120° | D. | 125° |
