题目内容
在△ABC中,AB=2,BC=5,AC=4,求sinC.
考点:解直角三角形,勾股定理
专题:
分析:首先设∠A对的边BC为a,∠B对的边为b,∠C对的边为c,根据任意三角形三边的关系c2=a2+b2-2abcosC,可求出cosC,然后根据sin2C+cos2C=1,求出sinC.
解答:解:设△ABC中∠A对的边BC为a,∠B对的边为b,∠C对的边为c,
则a=5,b=4,c=2,
c2=a2+b2-2abcosC,
∴22=52+42-2×5×4×cosC,
∴cosC=
=
,
又sin2C+cos2C=1,
∴sinC=
=
=
.
则a=5,b=4,c=2,
c2=a2+b2-2abcosC,
∴22=52+42-2×5×4×cosC,
∴cosC=
| 4-25-16 |
| -2×5×4 |
| 37 |
| 40 |
又sin2C+cos2C=1,
∴sinC=
| 1-cos2C |
1-(
|
| ||
| 40 |
点评:此题考查了学生对解三角形的掌握和运用.解答此题的关键根据任意三角形三边的关系c2=a2+b2-2abcosC,可求出cosC,再根据正弦定理得出sinC.

练习册系列答案
相关题目
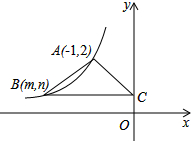 如图,在平面直角坐标系中,函数y=
如图,在平面直角坐标系中,函数y= 如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上任意一点,连接AP.若OA=10cm,OC=6cm,则AP的长度可能是
如图,AB是⊙O的弦,OC⊥AB于点C,连接OA、OB.点P是半径OB上任意一点,连接AP.若OA=10cm,OC=6cm,则AP的长度可能是