题目内容
已知二次函数y=-
x2+x+4.
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
| 1 |
| 2 |
(1)确定抛物线的开口方向、顶点坐标和对称轴;
(2)当x取何值时,y随x的增大而增大?当x取何值时,y随x的增大而减小?
考点:二次函数的性质
专题:
分析:(1)把二次函数解析式整理成顶点式形式,然后写出开口方向,顶点坐标和对称轴即可;
(2)根据二次函数的增减性解答即可.
(2)根据二次函数的增减性解答即可.
解答:解:(1)∵y=-
x2+x+4=-
(x-1)2+
,
∴抛物线开口向下,
顶点坐标为(1,
),
对称轴为直线x=1;
(2)当x<1时,y随x的增大而增大,
当x>1时,y随x的增大而减小.
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
∴抛物线开口向下,
顶点坐标为(1,
| 9 |
| 2 |
对称轴为直线x=1;
(2)当x<1时,y随x的增大而增大,
当x>1时,y随x的增大而减小.
点评:本题考查了二次函数的性质,主要利用了二次函数的开口方向,顶点坐标,对称轴以及二次函数的增减性,熟记性质是解题的关键.

练习册系列答案
相关题目
 在△ABC中,AD=BD,F是高AD和BE的交点,求证:BF=AC.
在△ABC中,AD=BD,F是高AD和BE的交点,求证:BF=AC.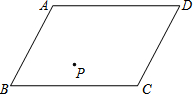 解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?
解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?