题目内容
若x1,x2是方程x2-3x=10的两根,则
(1)(x1+1)+(x2+1)= ;
(2)(x1+1),(x2+1)为两根的一元二次方程是 .
(1)(x1+1)+(x2+1)=
(2)(x1+1),(x2+1)为两根的一元二次方程是
考点:根与系数的关系
专题:
分析:(1)求出x1+x2=3,x1•x2=-10,(x1+1)+(x2+1)=x1+x2+2,代入求出即可;
(2)分别求出)(x1+1)+(x2+1)和(x1+1)(x2+1)的值,即可得出答案.
(2)分别求出)(x1+1)+(x2+1)和(x1+1)(x2+1)的值,即可得出答案.
解答:解:∵x2-3x=10,
∴x2-3x-10=0,
∵x1,x2是方程x2-3x=10的两根,
∴x1+x2=3,x1•x2=-10,
(1)(x1+1)+(x2+1)=x1+x2+2=3+2=5,
故答案为:5;
(2)∵(x1+1)+(x2+1)=5,(x1+1)(x2+1)=x1•x2+x1+x2+1=-10+3+1=-6,
∴以(x1+1),(x2+1)为两根的一元二次方程是x2-5x-6=0,
故答案为:x2-5x-6=0.
∴x2-3x-10=0,
∵x1,x2是方程x2-3x=10的两根,
∴x1+x2=3,x1•x2=-10,
(1)(x1+1)+(x2+1)=x1+x2+2=3+2=5,
故答案为:5;
(2)∵(x1+1)+(x2+1)=5,(x1+1)(x2+1)=x1•x2+x1+x2+1=-10+3+1=-6,
∴以(x1+1),(x2+1)为两根的一元二次方程是x2-5x-6=0,
故答案为:x2-5x-6=0.
点评:本题考查了根与系数,一元二次方程的应用,主要考查学生的理解能力和计算能力,题目比较好,难度适中.

练习册系列答案
相关题目
分式方程
-
=0的解为( )
| 3 |
| x |
| 2 |
| x-1 |
| A、x=1 | B、x=2 |
| C、x=3 | D、x=4 |
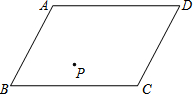 解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?
解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?