题目内容
11.某商场购进一批西服,进价为每套250元,原定每套以290元的价格销售,这样每天可销售200套,如果每套比原销售价降低10元销售,则每天可多销售100套,该商场为了确定销售价格,作了如下测算,请你参加测算,并由此归纳得出结论.(每套西服的利润=每套西服的销售价-每套西服的进价).(1)按原销售价销售,每天可获利润8000元;
(2)若每套降低10元销售,每天可获利润9000元;
(3)如果每套销售价降低10元,每天就多销售100套,每套销售价降低20元,每天就多销售200套,按这种方式:
若每套降低10x元(0≤x≤4,x为正整数).
①则每套的销售价格为(290-10x)元(用代数式表示);
②则每天可销售(200+100x)套西服(用代数式表示);
③则每天共可以获利润(40-10x)(200+100x)元(用代数式表示)
④根据以上的测算,如果你是该商场的经理,你将如何确定商场的销售方案,使每天的获利最大?
分析 (1)根据题目中数据可以求得按原销售价销售,每天可获得的利润;
(2)根据题目中数据可以求得每套降低10元销售,每天可获得的利润;
(3)①根据题意可以用代数式表示出每套的销售价格;
②根据题意可以用代数式表示出每天的销售量;
③根据题意可以用代数式表示出每天获得的利润;
④根据题意可以得到利润与销售价格之间的关系,从而可以解答本题.
解答 解:(1)按原销售价销售,每天可获利润为:(290-250)×200=8000(元),
故答案为:8000;
(2)若每套降低10元销售,每天可获利润为:(290-10-250)(200+100)=9000(元),
故答案为:9000;
(3)①由题意可得,
每套的销售价格为:(290-10x)元,
故答案为:(290-10x);
②每天可销售:(200+100x)套,
故答案为:(200+100x);
③每天共可以获利润为:(290-10x-250)(200+100x)=(40-10x)(200+100x)元,
故答案为:(40-10x)(200+100x);
④利润为W元,
则W=(40-10x)(200+100x)=-1000(x-1)2+9000,
∴当x=1时,W取得最大值,此时W=9000,
即每套比原销售价降低10元销售,可使每天的获利最大.
点评 本题考查列代数式、求函数的最值,解答此类问题的关键是明确题意,找出所求问题需要的条件,列出相应的代数式,利用二次函数的顶点式求函数的最值.

练习册系列答案
相关题目
4.已知抛物线y=ax2与双曲线y=-$\frac{2}{x}$交点的横坐标大于0,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-2 | D. | a<-2 |
19.解方程组:①$\left\{\begin{array}{l}{y=2x-1}\\{7x+5y=8}\end{array}\right.$,②$\left\{\begin{array}{l}{8x+6y=25}\\{17x-6y=48}\end{array}\right.$,在下列提供的两题解法中,较为简便的是( )
| A. | ①②均用代入法 | B. | ①②均用加减法 | ||
| C. | ①用代入法,②用加减法 | D. | ①用加减法,②用代入法 |
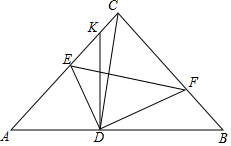 如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K.
如图,已知在等腰Rt△ABC中,∠C=90°,AB=6,若将△ABC翻折,且点C落在AB边上点D处,折痕EF分别交边AC,BC于点E和点F,过点D作DK⊥AB,交射线AC于点K. 如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.
如图,在网格图中,每个小正方形的顶点叫做格点,以格点为顶点的三角形叫做格点三角形,且每个小正方形的边长均为1,三角形ABC为一格点三角形,认真观察图形,请你求出三角形ABC的面积.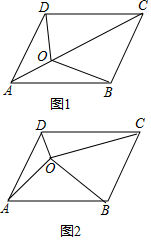 我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形.