题目内容
 如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是
如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是考点:全等三角形的判定
专题:开放型
分析:先求出∠ACB=∠DCE,再添加∠A=∠D,由已知条件BC=EC,即可证明△ABC≌△DEC.
解答:解:添加条件:∠A=∠D;
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
∴△ABC≌△DEC(AAS).
∵∠1=∠2,
∴∠1+∠ECA=∠2+∠ECA,
即∠ACB=∠DCE,
在△ABC和△DEC中,
|
∴△ABC≌△DEC(AAS).
点评:本题考查了全等三角形的判定;熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
 如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )| A、∠B=∠C |
| B、∠D=∠E |
| C、∠BAC=∠DAE |
| D、∠CAD=∠DAE |
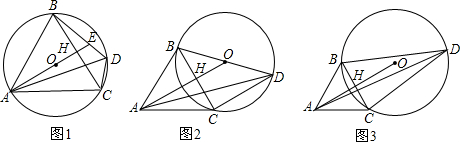
 如图,已知AB∥CD,AE∥CF,∠BAE与∠DCF有何关系?说说你的理由.
如图,已知AB∥CD,AE∥CF,∠BAE与∠DCF有何关系?说说你的理由.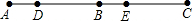 问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程.
问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程. 如图,由小正方形组成的格点图形,将图中某一个小正方形涂上阴影,与图中的三个阴影部分构成轴对称图形.
如图,由小正方形组成的格点图形,将图中某一个小正方形涂上阴影,与图中的三个阴影部分构成轴对称图形. 如图,已知AB∥CD,CE∥BF.求证:∠B=∠C.
如图,已知AB∥CD,CE∥BF.求证:∠B=∠C. 如图所示,直线AB,CD相交于点O,OE⊥AB,且∠DOE=40°,求∠AOC.
如图所示,直线AB,CD相交于点O,OE⊥AB,且∠DOE=40°,求∠AOC. 圆心相同,半径不同的两个圆叫同心圆.如图,以点O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C.若AB=4.BC=1,求圆环的面积.
圆心相同,半径不同的两个圆叫同心圆.如图,以点O为圆心的两个同心圆中,小圆的弦AB的延长线交大圆于点C.若AB=4.BC=1,求圆环的面积.