题目内容
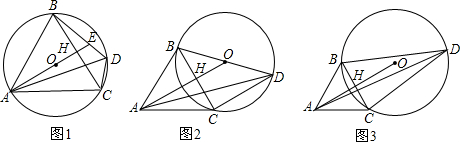
如图,△ABC为等边三角形.O为BC的中垂线AH上的动点,⊙O经过B,C两点,D为弧上一点,D,A两点在BC边异侧,连接AD,BD,CD.
(1)如图1,若⊙O经过点A,求证:BD+CD=AD;
(2)如图2,圆心O在BD上,若∠BAD=45°;求∠ADB的度数;
(3)如图3,若AH=OH,求证:BD2+CD2=AD2.
(1)如图1,若⊙O经过点A,求证:BD+CD=AD;
(2)如图2,圆心O在BD上,若∠BAD=45°;求∠ADB的度数;
(3)如图3,若AH=OH,求证:BD2+CD2=AD2.

考点:圆的综合题
专题:
分析:(1)利用图1,在DA上截取DM=DC,连接MC,由于⊙O经过点A,由∠ADC=∠ABC=60°,得出△MDC为等边三角形,易证△AMC≌△△BDC,可得AM=BD,即可得出结论,
(2)由点O在BD上,即BD为直径,可得∠BCD=90°,结合AH⊥BC,可得AO∥CD,∠OAD=∠ADC,由角的关系可得∠CAD=∠CDA,可得AC=DC,BC=DC,∠BDC=45°,即可求出∠ADB的值.
(3)利用图3,连接OB,OC,以点C为中心,把△ACD顺时针旋转60°,得到△BCN,连接DN,则AD=BN,DN=DC,∠ACB=∠DCN=60°,由AH=OH,可得△DCN,△BOC均为等边三角形,∠BOC=∠CDN=60°,∠BDC=30°,∠BDN=90°,由勾股定理可得BD2+CD2=BN2,即可得出BD2+CD2=AD2.
(2)由点O在BD上,即BD为直径,可得∠BCD=90°,结合AH⊥BC,可得AO∥CD,∠OAD=∠ADC,由角的关系可得∠CAD=∠CDA,可得AC=DC,BC=DC,∠BDC=45°,即可求出∠ADB的值.
(3)利用图3,连接OB,OC,以点C为中心,把△ACD顺时针旋转60°,得到△BCN,连接DN,则AD=BN,DN=DC,∠ACB=∠DCN=60°,由AH=OH,可得△DCN,△BOC均为等边三角形,∠BOC=∠CDN=60°,∠BDC=30°,∠BDN=90°,由勾股定理可得BD2+CD2=BN2,即可得出BD2+CD2=AD2.
解答:证明:(1)如图1,在DA上截取DM=DC,连接MC,
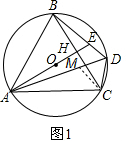
∵⊙O经过点A,
∴∠ADC=∠ABC=60°,
∴△MDC为等边三角形,
∴MC=DC,∠MCD=∠ACB=60°,
∴∠BCD=∠ACM,
又∵∠MAC=∠DBC,AC=BC,
∴△AMC≌△△BDC,
∴AM=BD,
∴BD+CD=AD,
(2)∵点O在BD上,即BD为直径,
∴∠BCD=90°,
∵AH⊥BC,
∴AO∥CD,
∴∠OAD=∠ADC,
∵∠BAD=45°,
∴∠OAD=∠CAD=15°,
∴∠CAD=∠CDA=15°,
∴AC=DC,
∴BC=DC,
∴∠BDC=45°,
∴∠ADB=30°.
(3)如图3,连接OB,OC,以点C为中心,把△ACD顺时针旋转60°,得到△BCN,连接DN,则AD=BN,DN=DC,∠ACB=∠DCN=60°.
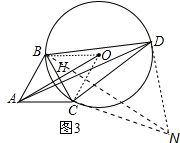
∵AH=OH,
∴△DCN,△BOC均为等边三角形,∠BOC=∠CDN=60°,
∴∠BDC=30°,
∴∠BDN=90°,
∴BD2+CD2=BN2,
∴BD2+CD2=AD2.

∵⊙O经过点A,
∴∠ADC=∠ABC=60°,
∴△MDC为等边三角形,
∴MC=DC,∠MCD=∠ACB=60°,
∴∠BCD=∠ACM,
又∵∠MAC=∠DBC,AC=BC,
∴△AMC≌△△BDC,
∴AM=BD,
∴BD+CD=AD,
(2)∵点O在BD上,即BD为直径,
∴∠BCD=90°,
∵AH⊥BC,
∴AO∥CD,
∴∠OAD=∠ADC,
∵∠BAD=45°,
∴∠OAD=∠CAD=15°,
∴∠CAD=∠CDA=15°,
∴AC=DC,
∴BC=DC,
∴∠BDC=45°,
∴∠ADB=30°.
(3)如图3,连接OB,OC,以点C为中心,把△ACD顺时针旋转60°,得到△BCN,连接DN,则AD=BN,DN=DC,∠ACB=∠DCN=60°.

∵AH=OH,
∴△DCN,△BOC均为等边三角形,∠BOC=∠CDN=60°,
∴∠BDC=30°,
∴∠BDN=90°,
∴BD2+CD2=BN2,
∴BD2+CD2=AD2.
点评:本题主要考查了圆的综合题,解题的关键是正确作出辅助线,利用等边三角形的性质求解.

练习册系列答案
相关题目
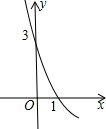 如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )
如图表示的是二次函数y=ax2+bx+c的图象的一部分,已知图象经过点(0,3)与(1,0),若s=a-b,则下列描述s的取值范围最合适的一个选项是( )| A、-3<s<3 | B、s>0 |
| C、s>3 | D、0<s<3 |
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
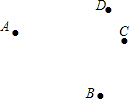 如图,已知平面上有四个点A,B,C,D四个村庄.
如图,已知平面上有四个点A,B,C,D四个村庄.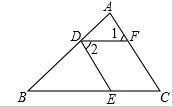 如图所示,点D,E,F分别在AB,BC,AC上.
如图所示,点D,E,F分别在AB,BC,AC上. 如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是
如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是