题目内容
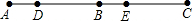 问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程.
问题:如图,线段AC上依次有D,B,E三点,其中点B为线段AC的中点,AD=BE,若DE=4,求线段AC的长.请补全以下解答过程.解:∵D,B,E三点依次在线段AC上,
∴DE=
∵AD=BE,
∴DE=DB+
∵DE=4,
∴AB=
∵
∴AC=2AB=
考点:两点间的距离
专题:推理填空题
分析:根据线段的和差,可得DE的长,根据等量代换,可得AB的长,根据线段中点的性质,可得答案.
解答:解:∵D,B,E三点依次在线段AC上,
∴DE=DB+BE.
∵AD=BE,
∴DE=DB+AD=AB.
∵DE=4,
∴AB=4.
∵点B为线段AC的中点,
∴AC=2AB=8,
故答案为:DB,BE;AD;4;点B为线段AC的中点;8.
∴DE=DB+BE.
∵AD=BE,
∴DE=DB+AD=AB.
∵DE=4,
∴AB=4.
∵点B为线段AC的中点,
∴AC=2AB=8,
故答案为:DB,BE;AD;4;点B为线段AC的中点;8.
点评:本题考查了两点间的距离,利用等量代换得出AB的值是解题关键,又利用了线段中点的性质.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
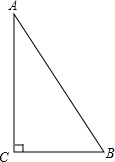
在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )
| A、4tan50° |
| B、4tan40° |
| C、4sin50° |
| D、4sin40° |
 如图,⊙O是△ABC的外接圆,若∠AOC=70°,则∠ABC的度数为( )
如图,⊙O是△ABC的外接圆,若∠AOC=70°,则∠ABC的度数为( )| A、140° | B、70° |
| C、30° | D、35° |
 已知,在△ABC中,∠C=90°,sinA=
已知,在△ABC中,∠C=90°,sinA=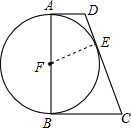 如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.
如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.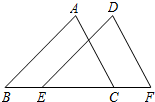 己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF. 如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是
如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是