题目内容
 如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )
如图所示,在△ABD和△ACE中,AB=AC,AD=AE.欲证△ABD≌△ACE,必须补充的条件是( )| A、∠B=∠C |
| B、∠D=∠E |
| C、∠BAC=∠DAE |
| D、∠CAD=∠DAE |
考点:全等三角形的判定
专题:
分析:补充∠EAD=∠BAC,由于∠EAD=∠BAC,可根据等式的性质得到∠EAD+∠DAC=∠BAC+∠DAC,即∠EAC=∠DAB,再加上条件AB=AC,AD=AE可用“SAS”可以判定△ABD≌△ACE.
解答:解:补充∠EAD=∠BAC,
∵∠EAD=∠BAC,
∴∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中,
,
∴△ABD≌△ACE(SAS).
故选C.
∵∠EAD=∠BAC,
∴∠EAD+∠DAC=∠BAC+∠DAC,
即∠EAC=∠DAB,
在△AEC和△ADB中,
|
∴△ABD≌△ACE(SAS).
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
以下列各组线段为边,能组成三角形的是( )
| A、2cm,3cm,5cm |
| B、3cm,3cm,6cm |
| C、5cm,8cm,2cm |
| D、4cm,5cm,6cm |
小明进行一次几何试验,他从A点出发,沿某一直线前进8m后向右转72°,再沿直线前进8m后,又向右转72°…,照这样走下去,他第一次回到出发点A点,请问他一共走了( )
| A、80m |
| B、45.6m |
| C、40m |
| D、他根本不可能回到出发A点 |
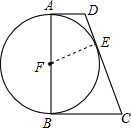 如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.
如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积. 如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是
如图,BC=EC,∠1=∠2,添加一个适当的条件使△ABC≌△DEC,则需添加的条件是 用两个直角边分别为a,b,斜边为c的全等直角三角形,按如图所示的拼法可拼出一个梯形,你能用这个图形的面积证明勾股定理吗?
用两个直角边分别为a,b,斜边为c的全等直角三角形,按如图所示的拼法可拼出一个梯形,你能用这个图形的面积证明勾股定理吗? 如图,AB⊥CD,EO⊥FO,垂足为O,则∠BOE的补角是
如图,AB⊥CD,EO⊥FO,垂足为O,则∠BOE的补角是