Question

19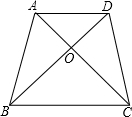．如图11，小强在纸上画出了两个三角形：△AOB与△DOC，点A，O，C在同一条直线上，点B，O，D在同一条直线上，且AB=DC，AC=DB．当他连接AD，BC后，得出了一个猜想：AD∥BC．你认为他的猜想正确吗？请说明理由．

Answer 1

分析 利用“SSS”证得△ABD≌△ACD，△ABC≌△BCD，可得到∠BAD=∠ADC，∠ABC=∠BCD，利用四边形四个内角和为360°，得出∠BAD+∠ADC+∠ABC+∠BCD=360°，推出∠BAD+∠ABC=180°即可得出结论．

解答 解：AD∥BC，正确．
理由：在△ABD和△ACD中，
$\left\{\begin{array}{l}{AB=DC}\\{BD=AC}\\{AD=DA}\end{array}\right.$，
∴△ABD≌△ACD，
∴∠BAD=∠ADC，
同理可得△ABC≌△BCD，
∴∠ABC=∠BCD，
∵∠BAD+∠ADC+∠ABC+∠BCD=360° 
∴∠BAD+∠ABC=180°，
∴AD∥BC．

点评 此题考查三角形全等的判定与性质，四边形的内角和，平行线的判定，掌握三角形全等的判定方法是解决问题的前提．