题目内容
9．把下列各分式的分子和分母中的多项式按x（或y）降幂排列，然后不改变分式的值，并使分子和分母中最高项的系数都是整数．（1）$\frac{-x}{1-2x{-x}^{2}}$；
（2）-$\frac{3y-{7y}^{2}}{5-7y{+y}^{2}}$．
分析 （1）根据分式的基本性质，把分子分母同时乘以-1，然后再按x的指数进行降幂排列即可；
（2）把分式前的符号移到分子上，然后再把分子分母按y降幂排列即可．
解答 解：（1）$\frac{-x}{1-2x{-x}^{2}}$=$\frac{x}{-1+2x+{x}^{2}}$=$\frac{x}{{x}^{2}+2x-1}$；
（2）-$\frac{3y-{7y}^{2}}{5-7y{+y}^{2}}$=$\frac{7{y}^{2}-3y}{{y}^{2}-7y+5}$．
点评 此题主要考查了分式的基本性质，关键是掌握分式的分子分母同时乘以同一个不为零的数，分式的值不变．
练习册系列答案
相关题目
20．已知2x2-3xy+y2=0，（xy≠0），则$\frac{x}{y}$的值是（ ）
| A． | 2，1 | B． | 1 | C． | $\frac{1}{2}$ | D． | 1，$\frac{1}{2}$ |
4．若$\root{3}{x}$+$\root{3}{-y}$=0，则x与y的关系是（ ）
| A． | x+y=0 | B． | x-y=0 | C． | x•y=0 | D． | x=y=0 |
14．某年，一些国家的服务出口额比上年的增长率如下：
这一年，上述六国中哪些国家的服务出口额增长了？哪些国家的服务出口额减少？哪国增长率最高？哪国增长率最低？
| 美国 | 德国 | 英国 | 中国 | 日本 | 意大利 |
| -3.4% | -0.9% | -5.3% | 2.8% | -7.3% | 7.0% |
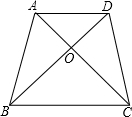如图11，小强在纸上画出了两个三角形：△AOB与△DOC，点A，O，C在同一条直线上，点B，O，D在同一条直线上，且AB=DC，AC=DB．当他连接AD，BC后，得出了一个猜想：AD∥BC．你认为他的猜想正确吗？请说明理由．