题目内容
1.解不等式(组)并将解集在数轴上表示出来(1)4x+5≥6x-3.
(2)$\left\{\begin{array}{l}{x-3(x-2)≤4}\\{\frac{1+2x}{3}>x-1}\end{array}\right.$
(3)$\left\{\begin{array}{l}{2x-1>x}\\{3-2x≥x+3}\end{array}\right.$
(4)$\left\{\begin{array}{l}{x-2>1}\\{3x+4>x}\end{array}\right.$.
分析 (1)通过移项、合并得-2x≥-8,然后把x的系数化为1即可得到不等式的解解,再用数轴表示出解集;
(2)分别解两个不等式得x≥1和x<4,然后根据大小小大中间找确定不等式组的解集,再利用数轴表示解集;
(3)分别解两个不等式得x>1和x≤0,然后根据大大小小找不到确定不等式组的解集,再利用数轴表示解集;
(4)分别解两个不等式得x>3和x>-2,然后根据同大取大确定不等式组的解集,再利用数轴表示解集.
解答 解:(1)移项得4x-6x≥-3-5,
合并得-2x≥-8,
系数化为1得x≤4,
用数轴表示为:
(2)$\left\{\begin{array}{l}{x-3(x-2)≤4①}\\{\frac{1+2x}{3}>x-1②}\end{array}\right.$,
解①得x≥1,
解②得x<4,
所以不等式组的解集为1≤x<4,
用数轴表示为:
(3)$\left\{\begin{array}{l}{2x-1>x①}\\{3-2x≥x+3②}\end{array}\right.$,
解①得x>1,
解②得x≤0,
所以不等式组无解,
用数轴表示为:
(4)$\left\{\begin{array}{l}{x-2>1①}\\{3x+4>x②}\end{array}\right.$,
解①得x>3,
解②得x>-2,
所以不等式组的解集为x>3,
用数轴表示为: .
.
点评 本题考查了解一元一次不等式组:一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
10.?ABCD中,相邻两角∠A、∠B有∠B-∠A=70°,则∠C的度数为( )
| A. | 55° | B. | 70° | C. | 155° | D. | 125° |
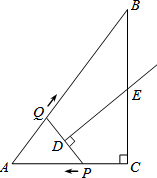 如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).
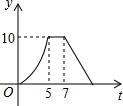
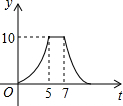
如图,在Rt△ABC中,∠C=90°,AC=3,AB=5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P,Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P,Q同时出发,当点Q到达点B时停止运动,点P也随之停止运动.设点P,Q运动的时间是t秒(t>0).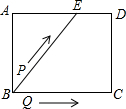 如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )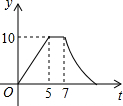

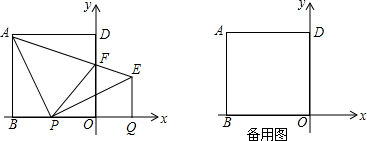
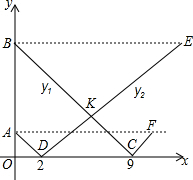 甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.
甲,乙两地相距630千米,客车从甲地出发向乙地匀速行驶,同时货车从乙地出发,向甲地匀速行驶,在甲乙两地间有一中途站P,货车的速度是客车的$\frac{3}{4}$,客、货车到P站的距离分别为y1、y2(千米),它们与行驶时间x(小时)之间的函数关系如图所示,则下列结论:①客车的速度为60千米/小时;②货车的速度为45千米/小时;③两车相遇的时间为6小时;④点E的坐标为(14,540).说法正确的个数有( )个.