题目内容
9.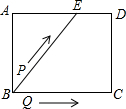 如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )
如图,矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,点P、Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒,△BPQ的面积为y cm2.则y与t的函数关系图象大致是( )| A. | 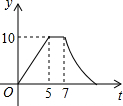 | B. | 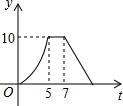 | C. |  | D. |  |
分析 分类讨论:①当0≤t<5,即点Q在线段BC上,点P在线段BE上;②当5≤t≤7,即点P在线段DE上,点Q在点C的位置,此时△BPQ的面积不变;③当7<t≤11,即点P在线段CD上,点Q在点C时.这三种情况下的函数图象,根据函数图象的性质进行判断.
解答 解:在矩形ABCD中,AB=4cm,AD=5cm,点E在AD上,且AE=3cm,
则在直角△ABE中,根据勾股定理得到BE=$\sqrt{A{B}^{2}+A{E}^{2}}=\sqrt{{4}^{2}+{3}^{2}}$=5cm,
①当0≤t≤5,即点P在线段BE上,点Q在线段BC上时,y=$\frac{2}{5}$t2,此时,该函数图象是开口向上的抛物线在第一象限的部分;
②当5≤t≤7,即点P在线段DE上,点Q在点C的位置,此时△BPQ的面积=$\frac{1}{2}BC•CD=\frac{1}{2}×5×4=10$,且保持不变;
③当7<t≤11,即点P在线段CD上,点Q在点C时,y=$\frac{1}{2}×5×[4-(t-7)]=-\frac{5}{2}t+\frac{55}{2}$,该函数图象是直线的一部分;
综上所述,B正确.
故选B
点评 本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

练习册系列答案
相关题目
18.弹簧挂上物体后会伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)上表反映的变量之间的关系中自变量是物体的质量,因变量是弹簧的长度.
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
| 物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度y(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
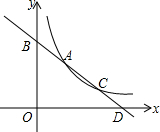 如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).
如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).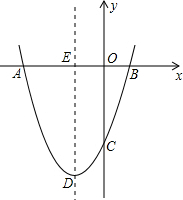 如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).
如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).
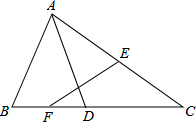 如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )
如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )