题目内容
6.计算(1)-23+(π-3.14)0-(1-2$\frac{1}{2}$)×(-$\frac{1}{2}$)-1
(2)(2x-y)(2x+y)-(x-3y)2.
分析 (1)原式第一项利用乘方的意义化简,第二项利用零指数幂法则计算,第三项利用负整数指数幂法则及乘法法则计算即可得到结果;
(2)原式利用平方差公式及完全平方公式化简,去括号合并即可得到结果.
解答 解:(1)原式=-8+1-(-1$\frac{1}{2}$)×(-2)=-8+1-3=-10;
(2)原式=4x2-y2-x2+6xy-9y2=3x2-10y2+6xy.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
11.已知点P(a,b)是平面直角坐标系中第四象限的点,则化简$\sqrt{b^2}$+|b-a|的结果是( )
| A. | a-2b | B. | a | C. | -a+2b | D. | -a |
18.弹簧挂上物体后会伸长,已知一弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系如表:
(1)上表反映的变量之间的关系中自变量是物体的质量,因变量是弹簧的长度.
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
| 物体的质量x(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度y(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当所挂物体是3kg时,弹簧的长度是13.5cm,不挂重物是12cm.
(3)直接写出y与x的关系式,并求出当弹簧长度为17cm时所挂物体质量.
15.在平面直角坐标系中,点(-3,-2)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
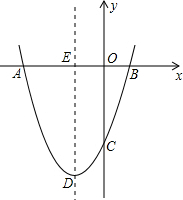 如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).
如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).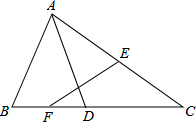 如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )
如图,在△ABC中,D是BC上一点,AB=AD,E、F分别是AC、BD的中点,EF=2,则AC的长是( )