题目内容
3.已知⊙O经过△ABC的三个顶点,AB=AC,圆心O到BC的距离为3,圆的半径为7,求腰长AB.分析 先根据勾股定理先求得BD的值,再根据勾股定理可求得AB的值.注意:圆心在内接三角形内时,AD=10cm;圆心在内接三角形外时,AD=4cm,再由勾股定理即可得出结论.
解答 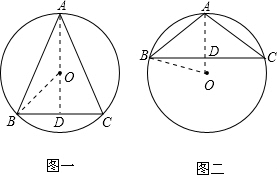 解:分圆心在内接三角形内和在内接三角形外两种情况讨论,
解:分圆心在内接三角形内和在内接三角形外两种情况讨论,
如图一,假若∠A是锐角,△ABC是锐角三角形,
连接OA,OB,
∵OD=3cm,OB=7cm,
∴AD=10cm,
∴BD=$\sqrt{{OB}^{2}-{OD}^{2}}$=2$\sqrt{10}$cm,
∵OD⊥BC,
∴BD=CD,
∵AB=AC,
∴AD⊥BC,
∴AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=2$\sqrt{35}$cm;
如图二,若∠A是钝角,则△ABC是钝角三角形,
和图一解法一样,只是AD=7-3=4cm,
∴AB=$\sqrt{{AD}^{2}+{BD}^{2}}$=2$\sqrt{14}$cm,
综上可得腰长AB=2$\sqrt{35}$cm或2$\sqrt{14}$cm.
点评 本题考查的是三角形的外接圆与外心,垂径定理和勾股定理,注意分圆心在内接三角形内和在内接三角形外两种情况讨论,有一定难度.

练习册系列答案
相关题目
7.已知三角形的两边a=3,b=7,则下列长度的四条线段中能作为第三边c的是( )
| A. | 3 | B. | 4 | C. | 7 | D. | 10 |
15.2013年,玉环县实现生产总值400.47亿元,在全国最具综合实力中小城市百强评选中名列第30位.要根据县政府的规划,预计到2015年,我县将实现生产总值467.12亿元.设我县实现生产总值的年平均增长率为x,则下面列出的方程中正确的是( )
| A. | 400.47(1+x)2=467.12 | B. | 467.12(1+x)2=400.47 | ||
| C. | 400.47(1+2x)2=467.12 | D. | 467.12(1+2x)2=400.47 |
12.点P(2,-1)向上平移2个单位长度后得到点P′,则点P′的坐标是( )
| A. | (4,-1) | B. | (4,1) | C. | (2,2) | D. | (2,1) |