题目内容
 如图,在?ABCD中,对角线AC、BD交于点O,AC=
如图,在?ABCD中,对角线AC、BD交于点O,AC=| 2 |
考点:平行四边形的性质
专题:证明题
分析:首先证明AB:AO=AC:AB,则△BAC∽△OAB证得,∠ABD=∠ACB,然后根据平行线的性质证得.
解答:证明:AC与BD相交于O
∵AC=
AB,AO=OC(平行四边形的性质)
∴AC=2AO,
∴AB=
AO,
∴AB:AO=AC:AB=
,
又∵∠BAC=∠OAB,
∴△BAC∽△OAB,
∴∠ABD=∠ACB,
∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
∴∠ABD=∠DAC.
∵AC=
| 2 |
∴AC=2AO,
∴AB=
| 2 |
∴AB:AO=AC:AB=
| 2 |
又∵∠BAC=∠OAB,
∴△BAC∽△OAB,
∴∠ABD=∠ACB,
∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
∴∠ABD=∠DAC.
点评:本题考查了平行四边形的性质以及相似三角形的判定与性质,正确证明△BAC∽△OAB是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
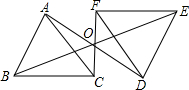 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )| A、点A与点D是对应点 |
| B、BO=EO |
| C、∠ACB=∠FDE |
| D、AB∥DE |
 310渔船在海上沿着正东南方向匀速航行,在A地观测到我渔船C在东北方向上的鱼场,若310船航向不变,航行20海里之后到达B处,此时观测到我渔船C在北偏东30°方向上,问:310渔船在航行多远,离我渔船的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,若有根号则保留根号)
310渔船在海上沿着正东南方向匀速航行,在A地观测到我渔船C在东北方向上的鱼场,若310船航向不变,航行20海里之后到达B处,此时观测到我渔船C在北偏东30°方向上,问:310渔船在航行多远,离我渔船的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,若有根号则保留根号) 如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数.
如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,AB于CD相交于点O,若∠A=40°,∠C=36°,求∠P的度数. 如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?
如图,某隧道的截面是一个半径为4米的半圆,一辆载有大型货物的卡车宽4米,高3.6米,这辆车能通过该隧道吗?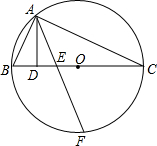 如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是
如图,△ABC内接于☉O,且BC是⊙O的直径,AD⊥BC于D,F是