题目内容
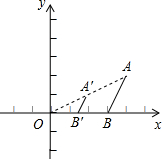
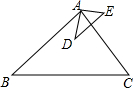如图所示，已知| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
| A、∠BAD=∠CAE |
| B、∠BAD＞∠CAE |
| C、∠BAD＜∠CAE |
| D、不能确定 |
考点：相似三角形的判定与性质
专题：
分析：由已知条件可证明△ABC∽△ADE，再利用角的和差可得到∠BAD=∠CAE．
解答：解：∵
=
=
，
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAD+∠DAC=∠DAC+∠CAE，
∴∠BAD=∠CAE，
故选A．
| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
∴△ABC∽△ADE，
∴∠BAC=∠DAE，
∴∠BAD+∠DAC=∠DAC+∠CAE，
∴∠BAD=∠CAE，
故选A．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的对应角相等是解题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
如图，D是Rt△ABC的直角边BC上的点，以BD为直径的⊙O交斜边AB于E，EC交⊙O于点F，BF的延长线交AC于点G，求证：FG•AC=FC•AE．一个盒子中装有9颗蓝色幸运星，n颗红色幸运星，从中任意取出一颗红色幸运星的频率为0.25，则n为（ ）
| A、1 | B、3 | C、5 | D、7 |
如图，在△ABC中，点D、E、F分别是边BC、CA、AB的中点，△DEF与△ABC是否位似？如果位似，找出位似中心？已知a+b=10，a3+b3=100，ab等于（ ）
| A、10 | B、20 | C、30 | D、40 |
在⊙O中，已知
=2
，则下列结论正确的是（ ）
 |
| AB |
|
| CD |
| A、AB＞2CD |
| B、AB=2CD |
| C、AB＜2CD |
| D、不能确定AB与2CD的大小关 |