题目内容
已知a+b=10，a3+b3=100，ab等于（ ）
| A、10 | B、20 | C、30 | D、40 |
考点：立方公式
专题：
分析：根据条件a+b=10，两边平方可求得a2+b2=100-2ab，再把条件a3+b3=100展成（a+b）和ab的形式，整体代入即可求得ab的值．
解答：解：∵a+b=10，
∴（a+b）2=a2+2ab+b2=100，
∴a2+b2=100-2ab，
∵a3+b3=（a+b）（a2-ab+b2）=（a+b）[（a+b）2-3ab）]=100，
故10（102-3ab）=100，
1000-30ab=100，
解得：ab=30．
故选：C．
∴（a+b）2=a2+2ab+b2=100，
∴a2+b2=100-2ab，
∵a3+b3=（a+b）（a2-ab+b2）=（a+b）[（a+b）2-3ab）]=100，
故10（102-3ab）=100，
1000-30ab=100，
解得：ab=30．
故选：C．
点评：此题主要考查了立方公式和完全平方公式的应用．要注意完全平方公式：（a±b）2=a2±2ab+b2，对a3+b3的准确分解是解本题的关键．
练习册系列答案
相关题目
阅读下面材料并回答问题：下列命题是真命题的是（ ）
| A、相等的角是对顶角 |
| B、三角形中有两个角的和大于180°，则这个三角形是锐角三角形 |
| C、对角线相等的四边形是矩形 |
| D、垂直平分线上的点到线段两端点的距离相等 |
如图，
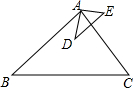如图所示，已知| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
| A、∠BAD=∠CAE |
| B、∠BAD＞∠CAE |
| C、∠BAD＜∠CAE |
| D、不能确定 |
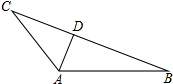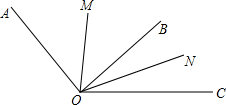如图，设相邻两个角∠AOB，∠BOC的角平分线分别为OM，ON，如果∠MON=α（α为常数），那么∠AOC的度数是否为一个固定值？若是，请说明理由，并求出∠AOC的度数；若不是，请说明理由．
如图所示，是一个由小立方体搭成的几何体的俯视图，小正方体中数字表示该位置的小立方块的个数，则它的主视图为（ ）
如图，AD是△ABC的角平分线，AD的垂直平分线交AD于点E，交BC的延长线于点F．