题目内容
一个盒子中装有9颗蓝色幸运星，n颗红色幸运星，从中任意取出一颗红色幸运星的频率为0.25，则n为（ ）
| A、1 | B、3 | C、5 | D、7 |
考点：利用频率估计概率
专题：
分析：由于一个盒子中装有9颗蓝色幸运星，n颗红色幸运星，根据从中任意取出一颗红色幸运星的频率为0.25列出方程，解方程即可求解．
解答：解：由题意，得
=0.25，
解得n=3．
故选B．
| n |
| 9+n |
解得n=3．
故选B．
点评：本题考查了利用频率估计概率，大量重复实验时，事件发生的频率在某个固定位置左右摆动，并且摆动的幅度越来越小，根据这个频率稳定性定理，可以用频率的集中趋势来估计概率，这个固定的近似值就是这个事件的概率．用频率估计概率得到的是近似值，随实验次数的增多，值越来越精确．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
下列命题中，真命题的个数是（ ）
（1）等腰三角形两腰上的高相等；
（2）在空间中，垂直于同一直线的两条直线平行；
（3）两条直线被第三条直线所截，内错角相等；
（4）一个角的两边与另一个角的两边分别平行，则这两个角相等．
（1）等腰三角形两腰上的高相等；
（2）在空间中，垂直于同一直线的两条直线平行；
（3）两条直线被第三条直线所截，内错角相等；
（4）一个角的两边与另一个角的两边分别平行，则这两个角相等．
| A、1 | B、2 | C、3 | D、4 |
如图，△ABC中点D、E分别在AB、AC上，且DE∥BC，已知BC=35，CE=15，DE=20，cosC=已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
则方程ax2+bx+c=0的正数解x1的取值范围是（ ）
| x | … | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
| A、0＜x1＜1 |
| B、1＜x1＜2 |
| C、2＜x1＜3 |
| D、3＜x1＜4 |
如图是某学校田径体育场一部分的示意图，跑道的长度是以该跑道的中心线来计算的，如以图中第一道的虚线部分来计算，第一条跑道每圈为400米，跑道分直道和弯道，直道为长相等的平行线段，弯道为同心的半圆型，弯道与直道相连接，已知直道BC的长86.96米，跑道的宽为l米．（π=3.14，结果精确到0.01）
下列命题是真命题的是（ ）
| A、相等的角是对顶角 |
| B、三角形中有两个角的和大于180°，则这个三角形是锐角三角形 |
| C、对角线相等的四边形是矩形 |
| D、垂直平分线上的点到线段两端点的距离相等 |
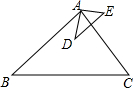如图所示，已知| AB |
| AD |
| BC |
| DE |
| AC |
| AE |
| A、∠BAD=∠CAE |
| B、∠BAD＞∠CAE |
| C、∠BAD＜∠CAE |
| D、不能确定 |