题目内容
1.已知在Rt△ABC中,∠C=90°,a+c=12,∠B=60°,解这个直角三角形.分析 根据在Rt△ABC中,∠C=90°,a+c=12,∠B=60°,可得∠A的度数,两条直角边的平方等于斜边的平方,从而可以解答这个直角三角形.
解答 解:∵在Rt△ABC中,∠C=90°,a+c=12,∠B=60°,
∴∠A=30°.
∴c=2a.
∴a=4,c=8.
∴b=$\sqrt{{c}^{2}-{a}^{2}}=\sqrt{{8}^{2}-{4}^{2}}=4\sqrt{3}$.
即:a=4,b=$4\sqrt{3}$,c=8,∠A=30°.
点评 本题考查解直角三角形,解题的关键是明确直角三角形的角角关系、边角关系.

练习册系列答案
相关题目
12.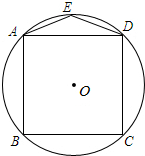 如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
 如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )
如图,正方形ABCD内接于⊙O,点E在劣弧$\widehat{AD}$上,则∠AED等于( )| A. | 100° | B. | 120° | C. | 135° | D. | 150° |
16.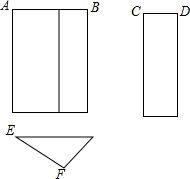 如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
 如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )| A. | 4 | B. | 4.5 | C. | 5 | D. | 6 |
6.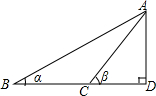 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )| A. | $\frac{tanα•tanβ}{tanβ-tanα}$•a | B. | ($\frac{1}{tanα}$-$\frac{1}{tanβ}$)•a | ||
| C. | $\frac{1}{tanα-tanβ}$•a | D. | (tanα-tanβ)•a |
11.下面四个等式中成立的是( )
| A. | (-a)2=-a2 | B. | -a3=a3 | C. | a2=|a|2 | D. | a3=|a|3 |
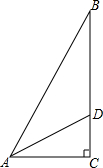 如图,在△ABC中,∠C=90°,∠A的平分线AD=4,∠DAC=30°,解直角△ABC.
如图,在△ABC中,∠C=90°,∠A的平分线AD=4,∠DAC=30°,解直角△ABC.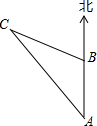 如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里.
如图,上午8时,一艘轮船从A处出发以每小时20海里的速度向正北航行,10时到达B处,则轮船在A处测得灯塔C在北偏西36°,航行到B处时,又测得灯塔C在北偏西72°,则从B到灯塔C的距离是40海里. 如图,⊙O的半径为5cm,点P在弦AB的延长线上,OP=6cm,∠P=30°,则AB=8cm.(请先补全图形再作答)
如图,⊙O的半径为5cm,点P在弦AB的延长线上,OP=6cm,∠P=30°,则AB=8cm.(请先补全图形再作答)