题目内容
6.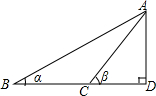 如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )
如图所示,已知∠ABD=α.△ACD=β,BC=a,则高AD为( )| A. | $\frac{tanα•tanβ}{tanβ-tanα}$•a | B. | ($\frac{1}{tanα}$-$\frac{1}{tanβ}$)•a | ||
| C. | $\frac{1}{tanα-tanβ}$•a | D. | (tanα-tanβ)•a |
分析 根据题意结合锐角三角函数关系用AD表示出DC的长,再表示出AD的长.
解答 解:由题意可得:tanβ=$\frac{AD}{DC}$,
则DC=$\frac{AD}{tanβ}$,
故tanα=$\frac{AD}{BC+DC}$=$\frac{AD}{a+\frac{AD}{tanβ}}$,
则AD=a•tanα+$\frac{tanα•AD}{tanβ}$,
解得:AD=$\frac{tanα•tanβ}{tanβ-tanα}$•a.
故选:A.
点评 此题主要考查了解直角三角形,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
10.我海军某舰队在一次军事演习中,一核潜艇在海下时而上升,时而下降,核潜艇的初始位置在海平面下1500m,下面是核潜艇在某段时间内的运动情况(把上升记为“+”,下降记为“-”单位:m):
(1)现在核潜艇在什么位置?
(2)假如核潜艇上升或下降1m核动力装置所提供的能量相当于21L汽油燃烧所产生的能量,那么在这一时刻内,核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
| 次数 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | 第6次 |
| 运动升降 | -1200 | -20 | 30 | 20 | 60 | -80 |
(2)假如核潜艇上升或下降1m核动力装置所提供的能量相当于21L汽油燃烧所产生的能量,那么在这一时刻内,核动力装置所提供的能量相当于多少升汽油燃烧所产生的能量?
17.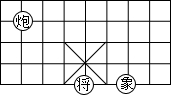 如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )
如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )
 如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )
如图,象棋棋盘上.若“将“位于点(1,-2)“象“位于点(3,-2),则“炮“位于点( )| A. | (-1,1) | B. | (-1,2) | C. | (-2,1) | D. | (-2,2) |
18.如图所示,下列四个选项中,不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
15. a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
 a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
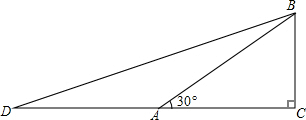 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?