题目内容
16.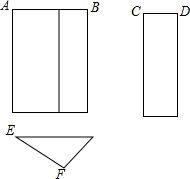 如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )
如图是一个三棱柱的三视图,若AB=5,CD=2,则EF的长度不可能是( )| A. | 4 | B. | 4.5 | C. | 5 | D. | 6 |
分析 根据三视图的对应情况可得出△EFG中EG上的高即为CD的长,进而根据勾股定理得到EF的取值范围,进而求出即可.
解答  解:如图,过点F作FQ⊥EG于点Q,
解:如图,过点F作FQ⊥EG于点Q,
由题意可得出:FQ=CD,
∵AB=5,CD=2,
∴EF=$\sqrt{E{Q}^{2}+F{Q}^{2}}$,
∵2<$\sqrt{E{Q}^{2}+F{Q}^{2}}$<$\sqrt{29}$,
∴EF的长度不可能是6.
故选:D.
点评 此题主要考查了由三视图判断几何体,体现了对空间想象能力方面的考查,根据已知条件得出FQ=CD是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.化简(a-b)2•(b-a)3的结果是( )
| A. | (a-b)5 | B. | (b-a)5 | C. | (a-b)6 | D. | b6-a6 |
6.下面四个式子中正确的是( )
| A. | -$\frac{1}{5}$<-5<5 | B. | 5<-5<-$\frac{1}{5}$ | C. | -5<5<-$\frac{1}{5}$ | D. | -5<-$\frac{1}{5}$<5 |
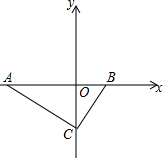 如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.
如图,在平面直角坐标系中,点A在x轴的负半轴上,点B在x轴的正半轴上.C在y轴的负半轴上,AC所在直线为y=kx-12.AC⊥BC.BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根.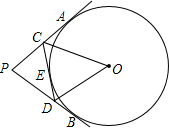 如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.
如图,PA,PB切⊙O于点A,B,点E是劣弧$\widehat{AB}$上一点,过E点作⊙O的切线交PA与C,交PB于D,若∠P=80°,∠DOC=50°.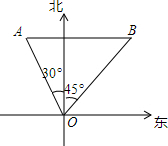 如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)
如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过3min到达哨所东北方向的B处,则该船的航速为每小时13.7km.(精确到0.1)