题目内容
12．
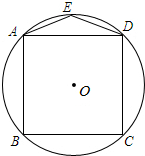如图，正方形ABCD内接于⊙O，点E在劣弧$\widehat{AD}$上，则∠AED等于（ ）| A． | 100° | B． | 120° | C． | 135° | D． | 150° |
分析 连接AO，DO，由正方形的性质知△AOD是等腰直角三角形，可得∠AOD=90°，由圆周角定理即可求出．
解答 
解：取圆上一点F，连接AO，DO，AF，DF，如图所示：
∵四边形ABCD为正方形，
∴∠AOD=90°，
∴∠AFD=$\frac{1}{2}∠$AOD=45°，
∴∠AED=135°，
故选C．
点评 本题利用了圆内接四边形的性质，正方形的性质，等腰直角三角形的性质及圆周角定理，熟记圆内接四边形的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
16．-11的倒数是（ ）
| A． | -$\frac{1}{11}$ | B． | -1 | C． | $\frac{1}{11}$ | D． | 11 |
如图，点G是Rt△ABC的重心，过点G作矩形GECF，当GF：GE=1：2时，则∠A的正切值．
17．
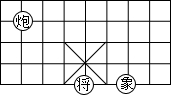如图，象棋棋盘上．若“将“位于点（1，-2）“象“位于点（3，-2），则“炮“位于点（ ）
如图，象棋棋盘上．若“将“位于点（1，-2）“象“位于点（3，-2），则“炮“位于点（ ）| A． | （-1，1） | B． | （-1，2） | C． | （-2，1） | D． | （-2，2） |
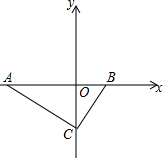如图，在平面直角坐标系中，点A在x轴的负半轴上，点B在x轴的正半轴上．C在y轴的负半轴上，AC所在直线为y=kx-12．AC⊥BC．BC的长的$\frac{1}{3}$倍是方程x2-3x-10=0的根．