题目内容
4.阅读下列解题过程:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)×(\sqrt{2}-1)}$=$\frac{\sqrt{2}-1}{(\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^{2}-(\sqrt{2})^{2}}$=$\sqrt{3}$-$\sqrt{2}$
请回答下列问题:
(1)归纳:观察上面的解题过程,请直接写出下列各式的结果.
①$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\sqrt{7}$-$\sqrt{6}$;②$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;
(2)应用:求$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+$\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{10}+\sqrt{9}}$的值;
(3)拓广:$\frac{1}{\sqrt{3}-1}$-$\frac{1}{\sqrt{5}-\sqrt{3}}$+$\frac{1}{\sqrt{7}-\sqrt{5}}$-$\frac{1}{\sqrt{9}-\sqrt{7}}$=-1.
分析 (1)①直接利用找出分母有理化因式进而化简求出答案;
②直接利用找出分母有理化因式进而化简求出答案;
(2)直接利用找出分母有理化因式进而化简求出答案;
(3)直接利用找出分母有理化因式进而化简求出答案.
解答 解:(1)①$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{1×(\sqrt{7}-\sqrt{6})}{(\sqrt{7}+\sqrt{6})(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$;
②$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\frac{1×(\sqrt{n}-\sqrt{n-1})}{(\sqrt{n}+\sqrt{n-1})(\sqrt{n}-\sqrt{n-1})}$=$\sqrt{n}$-$\sqrt{n-1}$;
故答案为:$\sqrt{7}$-$\sqrt{6}$;$\sqrt{n}$-$\sqrt{n-1}$;
(2)$\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+$\frac{1}{\sqrt{5}+\sqrt{4}}$+…+$\frac{1}{\sqrt{10}+\sqrt{9}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{10}$-$\sqrt{9}$
=$\sqrt{10}$-1;
(3)$\frac{1}{\sqrt{3}-1}$-$\frac{1}{\sqrt{5}-\sqrt{3}}$+$\frac{1}{\sqrt{7}-\sqrt{5}}$-$\frac{1}{\sqrt{9}-\sqrt{7}}$
=$\frac{\sqrt{3}+1}{(\sqrt{3}-1)(\sqrt{3}+1)}$-$\frac{\sqrt{5}+\sqrt{3}}{(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})}$+$\frac{\sqrt{7}+\sqrt{5}}{(\sqrt{7}-\sqrt{5})(\sqrt{7}+\sqrt{5})}$-$\frac{\sqrt{9}+\sqrt{7}}{(\sqrt{9}-\sqrt{7})(\sqrt{9}+\sqrt{7})}$
=$\frac{\sqrt{3}+1}{2}$-$\frac{\sqrt{5}+\sqrt{3}}{2}$+$\frac{\sqrt{7}+\sqrt{5}}{2}$-$\frac{\sqrt{9}+\sqrt{7}}{2}$
=$\frac{\sqrt{3}+1-\sqrt{5}-\sqrt{3}+\sqrt{7}+\sqrt{5}-\sqrt{9}-\sqrt{7}}{2}$
=-1.
故答案为:-1.
点评 此题主要考查了分母有理化,正确找出分母有理化因式是解题关键.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案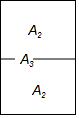 复印纸的型号A0,A1,A2,A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )
复印纸的型号A0,A1,A2,A3、A4等,它们之间存在着这样一种关系:将其中某一型号(如A3)的复印纸较长边的中点对折后,就能得到两张下一型号(A4)的复印纸,且得到的两个矩形都和原来的矩形相似(如图),那么这些型号的复印纸的长宽之比为( )| A. | $\sqrt{2}$:1 | B. | $\sqrt{3}$:1 | C. | 1:$\sqrt{2}$ | D. | 3:1 |
 同时抛掷两枚质地均匀的骰子,下列说法:(1)“两枚的点数都是3”的概率比“两枚的点数都是6”的概率大;(2)“两枚的点数相同”的概率是$\frac{1}{6}$;(3)“两枚的点数都是1”的概率最大;(4)“两枚的点数之和为奇数”与“两枚的点数之和为偶数”的概率相等.其中正确的是( )
同时抛掷两枚质地均匀的骰子,下列说法:(1)“两枚的点数都是3”的概率比“两枚的点数都是6”的概率大;(2)“两枚的点数相同”的概率是$\frac{1}{6}$;(3)“两枚的点数都是1”的概率最大;(4)“两枚的点数之和为奇数”与“两枚的点数之和为偶数”的概率相等.其中正确的是( )| A. | (1),(2) | B. | (3),(4) | C. | (1),(3) | D. | (2),(4) |
| A. | 0.2×1010 | B. | 2×1010 | C. | 2×109 | D. | 20×109 |
 如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,这是因为△ABC≌△DEC,而这个判定全等的依据是SAS.
如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出DE的长就等于AB的长,这是因为△ABC≌△DEC,而这个判定全等的依据是SAS.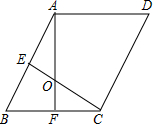 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,AF、CE相交于点O,则∠AOC=120°.
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,AF、CE相交于点O,则∠AOC=120°.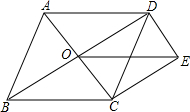 如图,在菱形ABCD中,对角线AC与BD相交于点O,CE∥BD,DE∥AC,连接OE.
如图,在菱形ABCD中,对角线AC与BD相交于点O,CE∥BD,DE∥AC,连接OE.