题目内容
14.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,若点A1的坐标为(3,1),则点A2016的坐标为(0,-2).分析 根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2016除以4,根据商和余数的情况确定点A2016的坐标即可.
解答 解:∵点A1的坐标为(3,1),
∴A2(-1+1,3+1),
即(0,4),A3(-4+1,0+1),
即(-3,1),A4(1-1,-3+1),
即(0,-2),A5(3,1),
…,
依此类推,每4个点为一个循环组依次循环,
∵2016÷4=504,
∴点A2016的坐标与A4的坐标相同,为(0,-2);
故答案为:(0,-2).
点评 此题考查点的坐标规律,读懂题目信息,理解“伴随点”的定义并求出每4个点为一个循环组依次循环是解题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
9.到三角形三个顶点的距离都相等的点是这个三角形的( )
| A. | 三条高的交点 | B. | 三条边的垂直平分线的交点 | ||
| C. | 三条中线的交点 | D. | 三条角平分线的交点 |
6.在(-1)2015,(-1)2016,-22,(-3)2四个数中,最大数与最小数的积等于( )
| A. | -4 | B. | -9 | C. | -36 | D. | -1 |
3.某电子原件厂家本周计划每天生产250件,由于工厂实行轮休,每天上班人数不一定相等,实际每天生产与计划相比情况如下表:
根据以上条件可知:
(1)本周六生产了多少件?
(2)本周总产量与计划相比,是增产还是减产?本周共生产了多少件?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周六生产了多少件?
(2)本周总产量与计划相比,是增产还是减产?本周共生产了多少件?
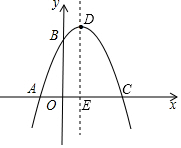 已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.
已知抛物线C1经过A(-1,0),B(0,3),C(3,0)三点,其顶点为点D,对称轴与x轴交于点E.