题目内容
13.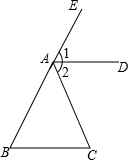 如图,∠CAE是△ABC的外角,
如图,∠CAE是△ABC的外角,①∠1=∠2,②AD∥BC,③AB=AC.
(1)请用①、②作为条件证明③;
(2)请用①、③作为条件证明②;
(3)作∠B的平分线交AD于F,分析△ABF的形状,并说明理由.
分析 (1)根据平行线的性质得到∠B=∠1,∠2=∠C,根据已知条件得到∠1=∠2,等量代换得到∠B=∠C,即可得到结论;
(2)根据等腰三角形的性质得到∠B=∠C,根据外角的性质得到∠EAC=∠1+∠2=∠B+∠C,推出∠EAC=2∠1=2∠B,于是得到∠1=∠B,根据平行线的判定定理即可得到结论;
(3)根据平行线的性质得到∠AFB=∠FBC,由角平分线的性质得到∠ABF=∠FBC,等量代换得到∠ABF=∠AFB.
解答 解:(1)命题:如果①②,那么③.证明如下:
∵AD∥BC,
∴∠B=∠1,∠2=∠C,
∵∠1=∠2,
∴∠B=∠C,
∴AB=AC;
(2)命题:如果①③,那么②.证明如下:
∵AB=AC,
∴∠B=∠C,
∵∠EAC=∠1+∠2=∠B+∠C,
∵∠1=∠2,
∴∠EAC=2∠1=2∠B,
∴∠1=∠B,
∴AD∥BC;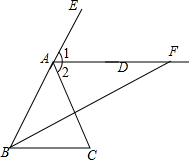
(3)△ABF是等腰三角形,
理由:∵AD∥BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
∴∠ABF=∠AFB,
∴△ABF是等腰三角形.
点评 本题考查了等腰三角形的判定和性质,平行线的判定和性质,角平分线的定义,熟练掌握各定理是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
17.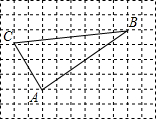 如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
 如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
 如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为m米,宽为n米
如图,在一长方形休闲广场的四角都设计一块半径相同的四分之一圆的花坛,若圆形的半径为r米,广场长为m米,宽为n米