题目内容
17.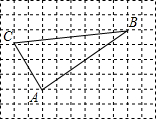 如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )
如图,网格纸中的小正方形的边长均为1,△ABC的三个顶点都在格点上,则△ABC是( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰三角形 |
分析 先根据勾股定理求出△ABC各边平方的值,再根据勾股定理的逆定理判断出△ABC的形状即可.
解答 解:由图形可知:AB2=42+62=52;AC2=22+32=13;BC2=82+12=65,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
故选B.
点评 本题考查的是勾股定理及其逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
12.下列各式由左边到右边的变形,是因式分解的是( )
| A. | 3x(x+y)+3x2+3xy | B. | -2x2-2xy=-2x(x+y) | C. | (x+5)(x-5)=x2-25 | D. | x2+x+1=x(x+1)+1 |
6.下列不等式不一定成立的是( )
| A. | -(a2+1)<0 | B. | 3a>2a | C. | a2≥0 | D. | a2+3>0 |
7.点E与点F的纵坐标相同,横坐标不同,则直线EF与y轴的关系是( )
| A. | 相交 | B. | 垂直 | C. | 平行 | D. | 以上都不正确 |
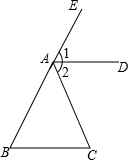 如图,∠CAE是△ABC的外角,
如图,∠CAE是△ABC的外角,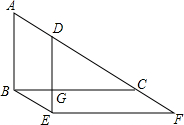 如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,
如图,直角三角形△ABC沿着AC所在直线平移得到△DEF,