题目内容
13.解不等式组$\left\{\begin{array}{l}k-3≤0\\ 2k+5>0\end{array}\right.$写出符合不等式组的整数解,并求出这些整数解中能使关于x的方程:2x+k=-1的解为非负数的概率.分析 解不等式组求得k的整数值,再找到使方程的解为非负数的k的值,根据概率公式求解可得.
解答 解:∵不等式组$\left\{\begin{array}{l}k-3≤0\\ 2k+5>0\end{array}\right.$的解集为-$\frac{5}{2}$<k≤3,
∴其整数解为k=-2,-1,0,1,2,3.
其中,当k=-2,-1时,方程2x+k=-1的解为非负数.
所以所求概率P=$\frac{2}{6}$=$\frac{1}{3}$.
点评 此题主要考查了解一元一次不等式组及解一元一次方程、概率的求法,掌握概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$是解题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
18.某服装专卖店销售的A款品牌西服去年销售总额为50000元,今年该款西服每件售价比去年便宜400元,若售出的件数相同,则该款西服销售总额将比去年降低20%,求今年该款西服的每件售价.若设今年该款西服的每件售价为x元,那么可列方程为( )
| A. | $\frac{50000}{x+400}$=$\frac{50000×(1-20%)}{x}$ | B. | $\frac{50000}{x}$=$\frac{50000×(1-20%)}{x+400}$ | ||
| C. | $\frac{50000}{x-400}$=$\frac{50000×(1-20%)}{x}$ | D. | $\frac{50000}{x}=\frac{50000×(1-20%)}{x-400}$ |
3. 2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
(1)频数分布表中a=60,b=0.05;本次比赛成绩的中位数会落在80≤x<90分数段;
(2)请补全频数分布直方图;
(3)该校安全知识竞赛成绩满分(100分)共有4人,其中男生2名,女生2名,为了激励学生增强安全意识,现需要从这4人中随机抽取2人介绍学习经验,请用“列表法”或“画树状图”,求恰好选到一男一女的概率.
 2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:
2017年南宁市教育局组织全市中小学时候参加安全知识网络竞赛,在安全知识竞赛结束后,赛后发现所有参赛学生会的成绩都高于50分.为了了解本次大赛的成绩分布情况,某校随机抽取了其中200名学生的成绩(成绩x取整数,总分为100分)作为样本进行统计分析,得到如下不完整的统计图表,请根据图标中的信息解答下列各题:| 成绩(分) | 频数 | 频数 |
| 50<x≤60 | 10 | b |
| 60<x≤70 | 20 | 0.10 |
| 70<x≤80 | 30 | 0.15 |
| 80<x≤90 | a | 0.30 |
| 90<x≤100 | 80 | 0.40 |
(2)请补全频数分布直方图;
(3)该校安全知识竞赛成绩满分(100分)共有4人,其中男生2名,女生2名,为了激励学生增强安全意识,现需要从这4人中随机抽取2人介绍学习经验,请用“列表法”或“画树状图”,求恰好选到一男一女的概率.
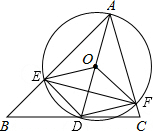 如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.
如图,在△ABC中,AB=10$\sqrt{2}$,∠BAC=60°,∠B=45°,点D是BC边上一动点,连接AD,以AD为直径作⊙O交边AB、AC于点E、F,连接OE、OF、DE、DF、EF.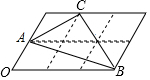 如图,6个形状、大小完全相同的菱形组成网格,已知菱形的一个角∠O为60°,A,B,C都在格点上,则tan∠ABC的值为$\frac{\sqrt{3}}{2}$.
如图,6个形状、大小完全相同的菱形组成网格,已知菱形的一个角∠O为60°,A,B,C都在格点上,则tan∠ABC的值为$\frac{\sqrt{3}}{2}$.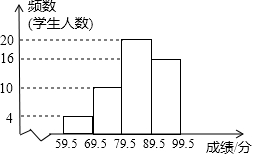 为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.
为增强学生环保意识,某中学组织全校2000名学生参加环保知识大赛,比赛成绩均为整数.从中抽取部分同学的成绩进行统计,并绘制成如图统计图.