题目内容
16.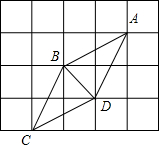 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 3 |
分析 首先过点C作CE⊥BD于点E,由勾股定理可求得BC,CD,BD的长,然后由三线合一求得BE的长,再利用勾股定理求得CE的长,继而求得答案.
解答 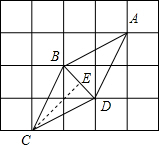 解:过点C作CE⊥BD于点E,
解:过点C作CE⊥BD于点E,
根据题意得:BC=CD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,BD=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴BE=$\frac{1}{2}$BD=$\frac{\sqrt{2}}{2}$,
∴CE=$\sqrt{B{C}^{2}-B{E}^{2}}$=$\frac{3\sqrt{2}}{2}$,
∴tan∠DBC=$\frac{CE}{BE}$=3.
故选D.
点评 此题考查了菱形的性质、等腰三角形的性质、勾股定理以及三角函数的定义.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
6.某县为大力推进义务教育均衡发展,加强学校“信息化”建设,计划用三年时间对全县学校的信息化设施和设备进行全面改造和更新.2016年县政府已投资2.5亿元人民币,若每年投资的增长率相同,预设2018年投资3.6亿元人民币,那么每年投资的增长率为( )
| A. | -20% | B. | 40% | C. | -220% | D. | 20% |
7.下列各数中,最小的数是( )
| A. | 0 | B. | -1 | C. | -$\sqrt{2}$ | D. | -2 |
11.若一个几何体的俯视图是圆,则这个几何体不可能是( )
| A. | 圆柱 | B. | 圆锥 | C. | 正方体 | D. | 球 |
1. O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )
 O为△ABC外心,∠BOC=40°,则∠BAC=( )
O为△ABC外心,∠BOC=40°,则∠BAC=( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
5.下列计算正确的是( )
| A. | a2•a3=a6 | B. | (b2)3=b6 | C. | (3m)2=6m2 | D. | x3÷x3=x |
 如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.
如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.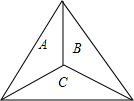 如图是一个正三角形的靶心,靶心为其三条对称轴的交点,飞镖随机地掷在靶上,则投到区域A或区域B的概率是$\frac{2}{3}$.
如图是一个正三角形的靶心,靶心为其三条对称轴的交点,飞镖随机地掷在靶上,则投到区域A或区域B的概率是$\frac{2}{3}$.