题目内容
4. 如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.
如图,矩形ABCD的边AB=3,AD=4,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连结EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连结CG.(1)求证:四边形EFCG是矩形;
(2)求tan∠CEG的值;
(3)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,求四边形EFCG面积的取值范围.
分析 (1)根据三个角是直角的四边形是矩形即可判断.
(2)只要证明∠CEG=∠ADB即可解决问题.
(3)首先证明S矩形EFCG=$\frac{3C{F}^{2}}{4}$,想办法求出CF的范围即可解决问题,只要求出CF的最大值以及最小值.
解答 解:(1)证明:∵CE为⊙O的直径,
∴∠CFE=∠CGE=90°,
∵EG⊥EF,
∴∠FEG=90°,
∴∠CFE=∠CGE=∠FEG=90°,
∴四边形EFCG是矩形.
(2)由(1)知四边形EFCG是矩形.
∴CF∥EG,
∴∠CEG=∠ECF,
∵∠ECF=∠EDF,
∴∠CEG=∠EDF,
在Rt△ABD中,AB=3,AD=4,
∴tan$∠BDA=\frac{AB}{AD}=\frac{3}{4}$,
∴tan∠CEG=$\frac{3}{4}$;
(3)∵四边形EFCG是矩形,
∴FC∥EG.
∴∠FCE=∠CEG,
∴tan∠FCE=tan∠CEG=$\frac{3}{4}$,
∵∠CFE=90°,
∴EF=$\frac{3}{4}$CF,
∴S矩形EFCG=$\frac{3C{F}^{2}}{4}$;
连结OD,如图2①,
∵∠GDC=∠CEG,∠FCE=∠FDE,
∴∠GDC=∠FDE.
∵∠FDE+∠CDB=90°,
∴∠GDC+∠CDB=90°,
∴∠GDB=90°.
(Ⅰ)当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′)处,如图2①所示.
此时,CF=CB=4.…(10分)
(Ⅱ)当点F在点D(F″)处时,直径F″G″⊥BD,
如图2②所示,
此时⊙O与射线BD相切,CF=CD=3.
(Ⅲ)当CF⊥BD时,CF最小,
如图2③所示.
S△BCD=$\frac{1}{2}$BC×CD=$\frac{1}{2}$BD×CF,
∴4×3=5×CF,
∴CF=$\frac{12}{5}$,
∴$\frac{12}{5}$≤CF≤4,
∵S矩形EFCG=$\frac{{3C{F^2}}}{4}$,
∴$\frac{3}{4}$×($\frac{12}{5}$)2≤S矩形EFCG≤$\frac{3}{4}$×42,
∴$\frac{108}{25}$≤S矩形EFCG≤12.
点评 本题考查四边形综合题、矩形的性质、锐角三角函数勾股定理等知识,解题的关键是学会添加辅助线,学会转化的思想,学会取特殊点特殊位置探究问题,属于中考压轴题.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案| A. | 1<AB<2 | B. | 2<AB<10 | C. | 4<AB<10 | D. | 4<AB<20 |
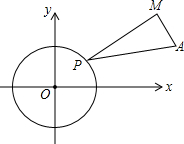 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
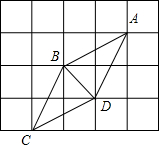 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 3 |
| A. | -8 | B. | 1 | C. | -4 | D. | $\frac{1}{4}$ |
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |


