题目内容
8.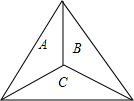 如图是一个正三角形的靶心,靶心为其三条对称轴的交点,飞镖随机地掷在靶上,则投到区域A或区域B的概率是$\frac{2}{3}$.
如图是一个正三角形的靶心,靶心为其三条对称轴的交点,飞镖随机地掷在靶上,则投到区域A或区域B的概率是$\frac{2}{3}$.
分析 由于靶心为其三条对称轴的交点,则A、B、C三个区域的面积相等,则可利用几何概率的计算方法求投到区域A或区域B的概率.
解答 解:投到区域A或区域B的概率=$\frac{2}{3}$.
故答案为$\frac{2}{3}$.
点评 此题主要考查了几何概率问题,用到的知识点为:概率=相应的面积与总面积之比.

练习册系列答案
相关题目
18.比-2小3的数是( )
| A. | -5 | B. | 1 | C. | -1 | D. | -6 |
19.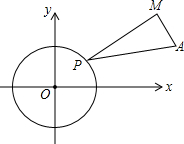 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
 如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )
如图,⊙O是以原点为圆心,半径为2的圆,点A(6,2),点P是⊙O上一动点,以线段PA为斜边构造直角△PAM,且cos∠MPA=$\frac{2\sqrt{2}}{3}$,现已知当点P在⊙O上运动时,保持∠MPA的大小不变,点M随着点P运动而运动且运动路径也形成一个圆,则该圆的半径是( )| A. | $\frac{1}{3}$ | B. | $\frac{2\sqrt{2}}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
16.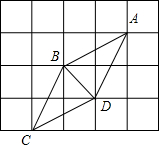 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 3 |
13.(0.125)2016×82016的值为( )
| A. | -8 | B. | 1 | C. | -4 | D. | $\frac{1}{4}$ |
20.下列计算正确的是( )
| A. | x2+x3=2x5 | B. | m8÷m2=m4 | C. | (m-n)2=m2-n2 | D. | (x2)3=x6 |
18.下列命题是真命题的是( )
| A. | 同旁内角相等,两直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 三角形的一个外角等于两个内角的和 | |
| D. | 两点确定一条直线 |
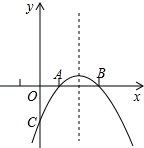 已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).
已知:如图所示,抛物线y=-x2+bx+c与x轴的两个交点分别为A(1,0),B(3,0).