题目内容
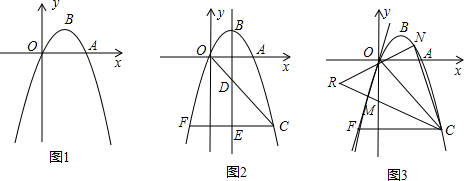
6.如图,已知二次函数y=ax2+bx+8(a≠0)的图象与x轴相交于点A(-2,0),B,与y轴相交于点C,tan∠ABC=2.(1)抛物线的解析式为y=-(x-1)2+9,其顶点D的坐标为(1,9);
(2)设置点CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,将抛物线沿其对称轴向上平移,使抛物线与线段EF总有公共点,试探究:抛物线最多可以向上平移多少个单位长度?
(3)在线段OB的处置平分线上是否存在点P,是的经过点P的直线PM垂直于直线CD,且与直线OP的夹角为75°,若存在直接写出点P的坐标;若不存在,请说明理由.
分析 (1)根据正切函数,可得B点坐标,根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据待定系数法,可得CD的解析式,根据自变量与函数值的对应关系,可得E.F点坐标,根据函数图象向上平移加,可得平移后的解析式,根据抛物线与线段有交点,可得抛物线的函数值小于E、F的纵坐标,可得答案;
(3)根据四边形的内角和,可得∠MPN的度数,根据角的和差,可得∠OPN,根据三角函数,可得PN的长,可得P点坐标.
解答 解:(1)当x=0时,y=8,即C(0,8),
由tan∠ABC=2,得B(4,0).
将A、B点坐标代入函数解析式,得
$\left\{\begin{array}{l}{4a-2b+8=0}\\{10a+4b+8=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
y=-x2+2x+8,
配方,得
y=-(x-1)2+9,顶点D(1,9),
故答案为:y=-(x-1)2+9,(1,9);
(2)设直线CD的解析式为y=kx+8,
将D(1,9)代入函数解析式,
得k=1,
直线CD的解析式为y=x+8,
当y=0时,x=-8,即E(-8,0),
当x=4时,y=4+8=12,即F(4,12).
设抛物线向上平移m各单位长度(m>0)后抛物线的解析式为y=-(x-1)2+9+m,
当x=-8时,y=m-72,当x=4时,y=m,
∵抛物线向上平移后与线段EF总有公共点,
∴m-72≤0或m≤12,
∴0<m≤72,
抛物线最多向上平移72个单位;
(3)存在符合条件的P点,P点坐标为(2,$\frac{2\sqrt{3}}{3}$)或(2,2$\sqrt{3}$);
由(2)得点E(-8,0),OC=OE=8,∠CEB=45°,在四边形EMPN中,∠MPN=180°-∠CEB=135°(∠PME,∠PNO都是直角)
①当∠OPM=75°时,∠OPN=135°-75°=60°
在Rt△OPN中,ON=$\frac{1}{2}$OB=2,sin∠PON=$\frac{PN}{ON}$=$\frac{\sqrt{3}}{3}$,PN=$\frac{\sqrt{3}}{3}$ON=$\frac{2\sqrt{3}}{3}$,即P(2,$\frac{2\sqrt{3}}{3}$);
②当∠OPQ=75°时,∠OPN=135°+75°-180°=30°,
在Rt△OPN中ON=$\frac{1}{2}$OB=2,PN=2$\sqrt{3}$,
综上所述,存在符合条件的点P,(2,$\frac{2\sqrt{3}}{3}$)或(2,2$\sqrt{3}$).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,利用配方法求函数顶点坐标;(2)利用图象与线段有交点得出不等式是解题关键;利用∠OPN是解题关键.

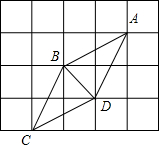 如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )
如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 3 |
| A. |  正方体 | B. |  长方体 | C. |  球 | D. |  圆锥 |
| A. | 同旁内角相等,两直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 三角形的一个外角等于两个内角的和 | |
| D. | 两点确定一条直线 |
| 分数/分 | 85 | 88 | 90 | 93 | 94 | 97 | 99 |
| 人数/人 | 1 | 7 | 11 | 10 | 13 | 7 | 1 |
| A. | 93分,94分 | B. | 90分,94分 | C. | 93分,93分 | D. | 94分,93分 |
 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )
如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上,如果∠1=23°,那么∠2的度数是( )| A. | 22° | B. | 23° | C. | 45° | D. | 68° |

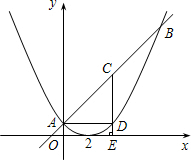 如图,已知以抛物线的顶点坐标为(2,0),直线y=x+1与该抛物线交于A、B两点,其中点A在y轴上.
如图,已知以抛物线的顶点坐标为(2,0),直线y=x+1与该抛物线交于A、B两点,其中点A在y轴上.