题目内容
18.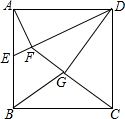 已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.
已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.
分析 先根据勾股定理和三角形的面积求出AF=$\frac{4}{\sqrt{5}}$,再利用相似三角形得出的比例式求出FM=$\frac{8}{5}$,AM=$\frac{4}{5}$,由线段的和差求出FP,FN,再用勾股定理得出FC,从而判断出DG=FP=$\frac{16}{5}$.进而用勾股定理得出CG,再用比例式得出GQ,CQ,最后用勾股定理即可.
解答 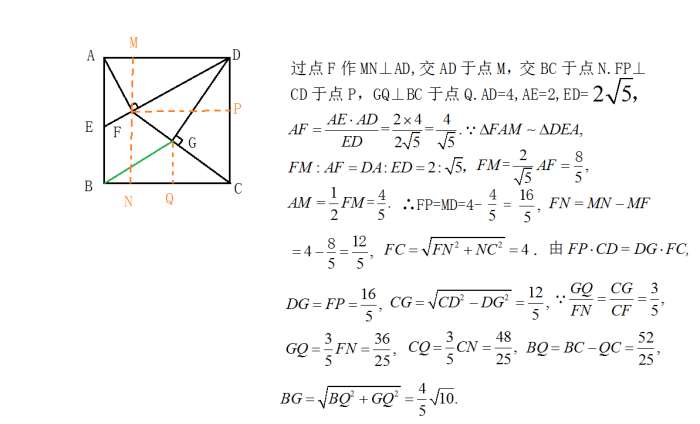 解:过点F作MN⊥AD,交AD于M,交BC于N,FP⊥CD于P,GQ⊥BC于Q,
解:过点F作MN⊥AD,交AD于M,交BC于N,FP⊥CD于P,GQ⊥BC于Q,
∵点E是AB中点,
∴AE=$\frac{1}{2}$AB=2,
根据勾股定理得,ED=2$\sqrt{5}$,
∵S△ADE=$\frac{1}{2}$DE×AF=$\frac{1}{2}$AD×AE,
∴AF=$\frac{AD×AE}{ED}$=$\frac{4}{\sqrt{5}}$,
∵AF⊥DE,
∴∠EAF+∠AEF=90°,
∵∠EAF+∠DAF=90°,
∴∠AEF=∠DAF,
∵∠AMF=∠EAD,
∴△FAM∽△DEA,
∴$\frac{FM}{AF}=\frac{AD}{ED}=\frac{2}{\sqrt{5}}$,$\frac{AM}{FM}=\frac{AE}{AD}=\frac{1}{2}$
∴FM=$\frac{2}{\sqrt{5}}$AF=$\frac{8}{5}$,
AM=$\frac{1}{2}$FM=$\frac{4}{5}$,
∴FP=MD=AD-AM=4-$\frac{4}{5}$=$\frac{16}{5}$,
FN=MN-MF=AB-MF=4-$\frac{8}{5}$=$\frac{12}{5}$,
根据勾股定理得,FC=$\sqrt{F{N}^{2}+N{C}^{2}}$=$\sqrt{F{N}^{2}+F{P}^{2}}$=4,
∵FP•CD=DG•FC,
∴DG=FP=$\frac{16}{5}$,
根据勾股定理得,CG=$\sqrt{C{D}^{2}-D{G}^{2}}$=$\frac{12}{5}$,
∵GQ∥FN,
∴$\frac{GQ}{FN}=\frac{CG}{CF}=\frac{3}{5}$,
∴GQ=$\frac{3}{5}$FN=$\frac{36}{25}$,CQ=$\frac{3}{5}$CN=$\frac{48}{25}$,
∴BQ=BC-CQ=$\frac{52}{25}$,
根据勾股定理,得BG=$\sqrt{B{Q}^{2}+G{Q}^{2}}$=$\frac{4}{5}\sqrt{10}$,
故答案为:$\frac{4}{5}\sqrt{10}$.
点评 此题是正方形的性质,主要考查了相似三角形的判定和性质,三角形的面积,勾股定理,解本题的关键是用勾股定理求出ED,FC,CG,BG,难点是作出辅助线,是一道比较难的中考常考题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案 如图,一个5×5的网格ABCD,在其形内有16个网格交点,分别以A、C为圆心,AB长(5个单位)为半径在形内画弧,两弧相交于点B、D,那么上述16个网格交点中位于两弧之间(不含弧上)的有( )
如图,一个5×5的网格ABCD,在其形内有16个网格交点,分别以A、C为圆心,AB长(5个单位)为半径在形内画弧,两弧相交于点B、D,那么上述16个网格交点中位于两弧之间(不含弧上)的有( )| A. | 8个 | B. | 9个 | C. | 10个 | D. | 12个 |
| A. | 同位角相等 | B. | 对顶角相等 | C. | 内错角相等 | D. | 同旁内角互补 |
| A. | 不变 | B. | 扩大为原来的3倍 | C. | 扩大为原来的9倍 | D. | 缩小到原来的$\frac{1}{3}$ |
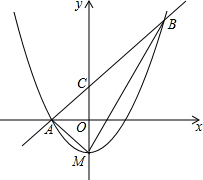 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A,B两点,且点A在x轴上,点B的横坐标为2,连接AM、BM.
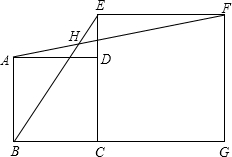 已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.
已知,如图,四边形ABCD和四边形ECGF都是正方形,连接BE、AF,求证:∠EHF=45°.