题目内容
2．已知四个数分别为p，q，r，s，且p＜q＜r＜s，若|p-r|=10，|p-s|=12，|q-s|=9，请在数轴上画出这四个数的大概位置，并利用该数轴求出|q-r|的值．分析 首先根据p＜q＜r＜s，以及p、r，p、s，q、s之间的距离，在数轴上画出这四个数的大概位置，然后根据|q-r|=|p-r|-|p-q|，求出|q-r|的值是多少即可．
解答 解：
，
|q-r|
=|p-r|-|p-q|
=|p-r|-（|p-s|-|q-s|）
=10-（12-9）
=10-3
=7
点评 此题主要考查了绝对值的含义和求法，以及数轴上两点之间的距离的求法，要熟练掌握．
练习册系列答案
相关题目
12．计算：3$\sqrt{12}$÷3$\sqrt{\frac{1}{3}}$-2$\sqrt{3}$的结果为（ ）
| A． | -2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 6-2$\sqrt{3}$ | D． | 36-2$\sqrt{3}$ |
如图，已知AD，AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90°，求：
10．下列各式成立的是（ ）
| A． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{23}$ | B． | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | C． | 5$\sqrt{3}$×4$\sqrt{2}$=20$\sqrt{6}$ | D． | 4$\sqrt{3}$×3$\sqrt{2}$=7$\sqrt{5}$ |
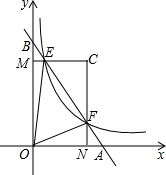在直角坐标系中，直线AB与x轴，y轴分别交于点A，B，与反比例函数y=$\frac{k}{x}$（k为常数，且k＞0）在第一象限的图象交于点E，F，过E作EM⊥y轴于M，过点F作FN⊥x轴于N，直线EM与FN交于点C．
14．-|-8|的相反数是（ ）
| A． | 8 | B． | -8 | C． | $\frac{1}{8}$ | D． | -$\frac{1}{8}$ |
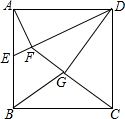已知正方形ABCD的边长为4，取AB边上的中点E，连接DE，过点A作AF⊥DE于点F，连按CF，过点D作DG⊥CF于点G，连接BG，则BG=$\frac{4}{5}\sqrt{10}$．