题目内容
13.如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.

分析 (1)如图1,先利用勾股定理计算出AG=5,再利用面积法和勾股定理计算出BF=$\frac{12}{5}$,AF=$\frac{16}{5}$,然后证明△ABF≌△DAE得到DE=AF=$\frac{16}{5}$;
(2)作CH⊥DE于H,如图2,先利用△ABF≌△DAE得到AE=BF=$\frac{12}{5}$,则EF=$\frac{4}{5}$,与(1)的证明方法一样可得△CDH≌△DAE,则CH=DE=$\frac{16}{5}$,DH=EF=$\frac{12}{5}$,EH=DE-DH=$\frac{4}{5}$,于是可判断EH=EF,接着证明△DEF≌△CHE,所以DF=CE,∠EDF=∠HCE,然后利用三角形内角和得到∠3=∠CHD=90°,从而判断DF⊥CE.
解答 解:(1)如图1,
∵四边形ABCD是正方形,
∴AD=AB=4,∠BAD=90°,
∵DE⊥AG,BF⊥AG,
∴∠AED=∠BFA=90°,
在Rt△ABG中,AG=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵$\frac{1}{2}$•AG•BF=$\frac{1}{2}$•AB•BG,
∴BF=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴AF=$\sqrt{A{B}^{2}-B{F}^{2}}$=$\sqrt{{4}^{2}-(\frac{12}{5})^{2}}$=$\frac{16}{5}$,
∵∠BAF+∠ABF=90°,∠BAF+∠DAE=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
$\left\{\begin{array}{l}{∠BFA=∠AED}\\{∠ABF=∠DAE}\\{AB=DA}\end{array}\right.$,
∴△ABF≌△DAE,
∴DE=AF=$\frac{16}{5}$;
(2)DF=CE,DF⊥CE.理由如下:
作CH⊥DE于H,如图2,
∵△ABF≌△DAE,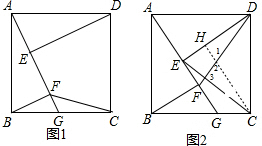
∴AE=BF=$\frac{12}{5}$,
∴EF=AF-AE=$\frac{4}{5}$,
与(1)的证明方法一样可得△CDH≌△DAE,
∴CH=DE=$\frac{16}{5}$,DH=EF=$\frac{12}{5}$,
∴EH=DE-DH=$\frac{4}{5}$,
∴EH=EF,
在△DEF和△CHE中
$\left\{\begin{array}{l}{DE=CH}\\{∠DEF=∠CHE}\\{EF=HE}\end{array}\right.$,
∴△DEF≌△CHE,
∴DF=CE,∠EDF=∠HCE,
∵∠1=∠2,
∴∠3=∠CHD=90°,
∴DF⊥CE.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.解决问题的关键是利用三角形全等证明线段相等.

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案 如图,点A(2,t)在第一象限,OA与x轴所夹锐角为α,tanα=2,则t值为( )
如图,点A(2,t)在第一象限,OA与x轴所夹锐角为α,tanα=2,则t值为( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
 如图,己知直线AB为函数y=2x+6的图象.
如图,己知直线AB为函数y=2x+6的图象.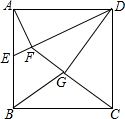 已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.
已知正方形ABCD的边长为4,取AB边上的中点E,连接DE,过点A作AF⊥DE于点F,连按CF,过点D作DG⊥CF于点G,连接BG,则BG=$\frac{4}{5}\sqrt{10}$.