题目内容
7.已知函数y=$\frac{1}{2}$x2+2x+1,用配方法把它写成y=a(x-h)2+k的形式为$\frac{1}{2}$(x+2)2-1;当x>-2时,其函数值y随x的增大而增大;当x<-2时,其函数值y随x的增大而减小.分析 先把函数化为顶点式的形式,求出顶点坐标,根据二次函数的增减性即可得出结论.
解答 解:∵y=$\frac{1}{2}$x2+2x+1=$\frac{1}{2}$(x2+4x)+1=$\frac{1}{2}$(x2+4x+4)-1=$\frac{1}{2}$(x+2)2-1,
∴函数图象的顶点坐标为(-2,-1),对称轴为直线x=-2,
∴当x>-2时,其函数值y随x的增大而增大;当x<-2时,其函数值y随x的增大而减小.
故答案为:y=$\frac{1}{2}$(x+2)2-1,>-2,<-2.
点评 本题考查的是二次函数的三种形式,熟记二次函数的顶点式及二次函数的增减性是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?
如图,点B在点A北偏东35度的方向,点C在点B北偏西55度的方向,且BC=10m,问点C到直线AB的距离是多少?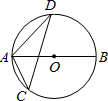 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.
如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=52°,则∠BAD=38°.