题目内容
如图1,⊙O在直角坐标系中是一个以原点为圆心,半径为4的圆,AB是过圆心O的直径,点P从点B出发沿圆O做匀速运动,过点P作PC垂直于半径AB,PC的长度随着点P的运动而变化.(各组数据已标出)
(1)当P点的位置如图所示时,求∠OPC和∠POC的度数.
(2)当P点的位置如图所示时,求PC的值.
(3)探究:PC的长度随着∠BOP的变化而变化,设PC的值为y,∠BOP为x,
并规定:①PC在x轴上方记为正,在x轴下方记为负;②逆时针旋转得到的角度记为正,顺时针旋转得到的角度记为负;③π=180°,
π=900.请写出y关于x的函数关系式,以及x的取值范围.(直接写出答案)
(4)在图2试画出第(3)题中函数的图象.
(5)求出该函数图象的对称轴.(直接写出答案,答案请用含有π的式子表示)
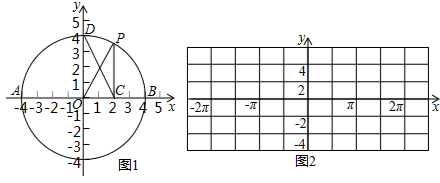
(1)当P点的位置如图所示时,求∠OPC和∠POC的度数.
(2)当P点的位置如图所示时,求PC的值.
(3)探究:PC的长度随着∠BOP的变化而变化,设PC的值为y,∠BOP为x,
并规定:①PC在x轴上方记为正,在x轴下方记为负;②逆时针旋转得到的角度记为正,顺时针旋转得到的角度记为负;③π=180°,
| 1 |
| 2 |
(4)在图2试画出第(3)题中函数的图象.
(5)求出该函数图象的对称轴.(直接写出答案,答案请用含有π的式子表示)

考点:圆的综合题,勾股定理,轴对称图形,锐角三角函数的定义
专题:综合题
分析:(1)利用三角函数就可解决问题.
(2)运用勾股定理即可解决问题.
(3)根据条件中的规定就可得到y=4sinx,其中x为任意实数.
(4)可用描点法画出(3)中函数的图象.
(5)由图可知:该图象的对称轴有无数个,这些对称轴方程分别为…,x=-
,x=-
,x=
,x=
,…,从而可归纳出该图象的对称轴方程.
(2)运用勾股定理即可解决问题.
(3)根据条件中的规定就可得到y=4sinx,其中x为任意实数.
(4)可用描点法画出(3)中函数的图象.
(5)由图可知:该图象的对称轴有无数个,这些对称轴方程分别为…,x=-
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
解答: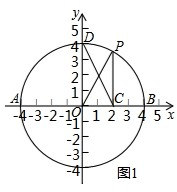 解:(1)如图1,则有OP=4,OC=2,∠PCO=90°.
解:(1)如图1,则有OP=4,OC=2,∠PCO=90°.
∴sin∠OPC=
=
=
.
∴∠OPC=30°.
∴∠POC=60°.
(2)如图1,
∵OP=4,OC=2,∠PCO=90°,
∴PC=
=2
.
∴PC的值为2
.
(3)由题可知:y=OP•sin∠BOP=4sinx,其中x为任意实数.
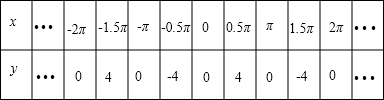
(4)列表
描点,连线,如图2.
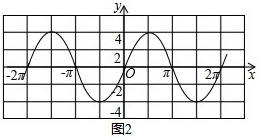
(5)由图2可知:该函数图象的对称轴有无数个,
这些对称轴方程为…,x=-
,x=-
,x=
,x=
,…
其中x=-
=-2π+
,
x=-
=-π+
,
x=
=0•π+
,
x=
=π+
…
归纳:该函数图象的对称轴方程为x=kπ+
(k为整数).
 解:(1)如图1,则有OP=4,OC=2,∠PCO=90°.
解:(1)如图1,则有OP=4,OC=2,∠PCO=90°.∴sin∠OPC=
| OC |
| OP |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠OPC=30°.
∴∠POC=60°.
(2)如图1,
∵OP=4,OC=2,∠PCO=90°,
∴PC=
| OP2-OC2 |
| 3 |
∴PC的值为2
| 3 |
(3)由题可知:y=OP•sin∠BOP=4sinx,其中x为任意实数.
(4)列表

描点,连线,如图2.

(5)由图2可知:该函数图象的对称轴有无数个,
这些对称轴方程为…,x=-
| 3π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
其中x=-
| 3π |
| 2 |
| π |
| 2 |
x=-
| π |
| 2 |
| π |
| 2 |
x=
| π |
| 2 |
| π |
| 2 |
x=
| 3π |
| 2 |
| π |
| 2 |
…
归纳:该函数图象的对称轴方程为x=kπ+
| π |
| 2 |
点评:本题与高中知识相接轨,考查了三角函数的定义、特殊角的三角函数值、勾股定理、轴对称图形等知识,还考查了阅读、操作、归纳、探究等能力,是一道好题.

练习册系列答案
相关题目
 已知实数a、b在数轴上的位置如图:
已知实数a、b在数轴上的位置如图: 如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D.
如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D.