题目内容
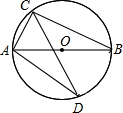 如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D.
如图,点C为圆上一点,⊙O直径AB为10cm,∠ACB的平分线交⊙O于D.(1)若弦AC为6cm,求BC、AD的长.
(2)当点C在⊙O上运动时,试判断点D是否随着点C的变化而变化?若改变,设AC=x,AD=y,请建立y与x的关系式;若不变,请说明理由.
考点:圆周角定理,勾股定理,圆心角、弧、弦的关系
专题:综合题
分析:(1)连接OD,由AB是⊙O的直径得∠ACB=90°,然后运用勾股定理就可求出BC长;根据圆周角定理可得∠AOD=2∠ACD=90°,在Rt△AOD中运用勾股定理就可求出AD长.
(2)在(1)中已证到∠AOD=∠BOD=90°,根据“在同圆或等圆中,相等的圆心角所对的弧相等”可得
=
,即可解决问题.
(2)在(1)中已证到∠AOD=∠BOD=90°,根据“在同圆或等圆中,相等的圆心角所对的弧相等”可得
 |
| AD |
 |
| BD |
解答:解: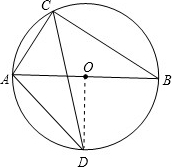 (1)连接OD,如图所示.
(1)连接OD,如图所示.
∵AB是⊙O的直径,
∴∠ACB=90°.
∵AB=10,AC=6,
∴BC=8.
∵CD平分∠ACB,
∴∠ACD=∠BCD=
∠ACB=45°.
∴∠AOD=2∠ACD=90°,∠BOD=2∠BCD=90°.
在Rt△AOD中,
AD=
=
=5
.
∴BC的长为8cm、AD的长为5
cm.
(2)当点C在上半圆上运动时,点D不变,在下半圆的中点.
理由如下:
∵∠AOD=∠BOD=90°(已证),
∴
=
.
∴点D是下半圆的中点.
 (1)连接OD,如图所示.
(1)连接OD,如图所示.∵AB是⊙O的直径,
∴∠ACB=90°.
∵AB=10,AC=6,
∴BC=8.
∵CD平分∠ACB,
∴∠ACD=∠BCD=
| 1 |
| 2 |
∴∠AOD=2∠ACD=90°,∠BOD=2∠BCD=90°.
在Rt△AOD中,
AD=
| AO2+OD2 |
| 52+52 |
| 2 |
∴BC的长为8cm、AD的长为5
| 2 |
(2)当点C在上半圆上运动时,点D不变,在下半圆的中点.
理由如下:
∵∠AOD=∠BOD=90°(已证),
∴
 |
| AD |
 |
| BD |
∴点D是下半圆的中点.
点评:本题考查了圆周角定理、勾股定理、圆心角与圆弧的关系、角平分线的定义等知识,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,已知:BD,CE是△ABC的两条高.
如图,已知:BD,CE是△ABC的两条高.
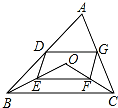 点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.