题目内容
解下列方程:
(1)6x2-8x+1=2;
(2)(2y-1)2=(3y+3)2.
(1)6x2-8x+1=2;
(2)(2y-1)2=(3y+3)2.
考点:解一元二次方程-因式分解法,解一元二次方程-公式法
专题:
分析:(1)利用公式法直接求出方程的根即可;
(2)利用平方差公式因式分解进而求出方程的根即可.
(2)利用平方差公式因式分解进而求出方程的根即可.
解答:解:(1)6x2-8x+1=2
整理得:6x2-8x-1=0,
b2-4ac=64+24=88>0,
故x=
=
,
x1=
,x2=
;
(2)(2y-1)2=(3y+3)2
[(2y-1)+(3y+3)][(2y-1)-(3y+3)]=0
(5y+2)(-y-4)=0
解得:y1=-
,y2=-4.
整理得:6x2-8x-1=0,
b2-4ac=64+24=88>0,
故x=
8±
| ||
| 4×6 |
4±
| ||
| 12 |
x1=
4+
| ||
| 12 |
4-
| ||
| 12 |
(2)(2y-1)2=(3y+3)2
[(2y-1)+(3y+3)][(2y-1)-(3y+3)]=0
(5y+2)(-y-4)=0
解得:y1=-
| 2 |
| 5 |
点评:此题主要考查了公式法以及因式分解法解方程,熟练记忆公式是解题关键.

练习册系列答案
相关题目
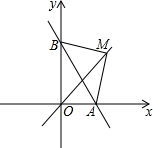 如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a-2)2+
如图,在平面直角坐标系中,A(a,0),B(0,b),且a、b满足(a-2)2+
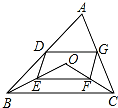 点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.
点O是三角形ABC所在平面内一动点,连接OB、OC,并将AB、OB、OC、AC中点D、E、F、G,依次连接起来,设DEFG能构成四边形.